Mathématiques > Probabilités et Statistiques > Statistiques > Analyse de données

Régression linéaire simple

Apprendre à modéliser la relation entre deux variables continues à l'aide de la régression linéaire simple. Ce guide explique comment construire un modèle, interpréter les coefficients et évaluer sa performance.

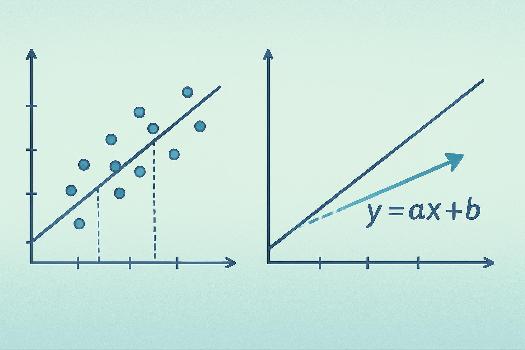
Introduction à la régression linéaire

La régression linéaire est une technique statistique utilisée pour modéliser la relation entre une variable dépendante (ou variable à expliquer) et une ou plusieurs variables indépendantes (ou variables explicatives). Dans le cas de la régression linéaire simple, nous avons une seule variable indépendante et une variable dépendante. L'objectif est de trouver la droite qui ajuste le mieux les données, permettant ainsi de prédire les valeurs de la variable dépendante à partir des valeurs de la variable indépendante.

L'équation de la droite

L'équation d'une droite en régression linéaire simple est donnée par : y = ax + b, où :

  • y est la variable dépendante.
  • x est la variable indépendante.
  • a est la pente de la droite (le coefficient de régression), qui indique de combien y change pour chaque unité de changement de x.
  • b est l'ordonnée à l'origine (l'intercept), qui est la valeur de y lorsque x est égal à 0.
Le but de la régression linéaire est d'estimer les valeurs de a et b qui minimisent la différence entre les valeurs observées de y et les valeurs prédites par le modèle.

Estimation des coefficients

Les coefficients a (pente) et b (ordonnée à l'origine) sont estimés à partir des données observées. Les méthodes courantes pour l'estimation incluent la méthode des moindres carrés ordinaires (MCO). La méthode MCO vise à minimiser la somme des carrés des résidus (la différence entre les valeurs observées et les valeurs prédites). Les formules pour calculer a et b sont les suivantes:

  • a = Cov(x, y) / Var(x), où Cov(x, y) est la covariance entre x et y, et Var(x) est la variance de x.
  • b = moyenne(y) - a * moyenne(x).
Ces formules permettent de calculer les coefficients qui minimisent l'erreur quadratique moyenne du modèle.

Interprétation des coefficients

L'interprétation des coefficients est cruciale pour comprendre la relation entre les variables. La pente a indique la variation de la variable dépendante pour chaque unité de variation de la variable indépendante. Par exemple, si a est égal à 2, cela signifie que pour chaque augmentation d'une unité de x, y augmente en moyenne de 2 unités. L'ordonnée à l'origine b représente la valeur de la variable dépendante lorsque la variable indépendante est égale à zéro. Cependant, il est important de noter que l'interprétation de b doit être effectuée avec prudence, car elle peut ne pas avoir de sens pratique si la valeur zéro de la variable indépendante n'est pas dans la plage des données observées.

Évaluation du modèle

Plusieurs métriques peuvent être utilisées pour évaluer la performance du modèle de régression linéaire :

  • Coefficient de détermination (R²) : Mesure la proportion de la variance de la variable dépendante qui est expliquée par le modèle. R² varie de 0 à 1, où une valeur proche de 1 indique un bon ajustement du modèle aux données.
  • Erreur quadratique moyenne (EQM) : Mesure la moyenne des carrés des résidus. Une EQM plus faible indique une meilleure performance du modèle.
  • Test de signification : Vérifie si les coefficients de régression sont statistiquement significatifs. Un test de signification (test t) est effectué pour chaque coefficient.
Une analyse des résidus (différence entre les valeurs observées et les valeurs prédites) est également importante pour vérifier les hypothèses du modèle (normalité des résidus, homoscédasticité).

Exemple concret

Supposons que vous voulez étudier la relation entre le nombre d'heures d'étude (x) et la note obtenue à un examen (y). Vous collectez des données sur un échantillon d'étudiants et vous ajustez un modèle de régression linéaire simple. Vous obtenez l'équation suivante : y = 5x + 60. Cela signifie que pour chaque heure d'étude supplémentaire, la note à l'examen augmente en moyenne de 5 points. La note à l'examen serait de 60 si l'étudiant n'étudiait pas du tout. Vous calculez également le coefficient de détermination R² et obtenez une valeur de 0.8. Cela signifie que 80% de la variance de la note à l'examen est expliquée par le nombre d'heures d'étude.

Ce qu'il faut retenir

  • La régression linéaire simple modélise la relation entre deux variables continues.
  • L'équation de la droite est y = ax + b, où a est la pente et b est l'ordonnée à l'origine.
  • Les coefficients sont estimés à partir des données à l'aide de méthodes comme la MCO.
  • L'interprétation des coefficients est cruciale pour comprendre la relation entre les variables.
  • Plusieurs métriques (R², EQM, tests de signification) sont utilisées pour évaluer la performance du modèle.

← Probabilités conditionnelles : Comprendre et appliquer Variables aléatoires : discrètes et continues →

FAQ

  • Quelle est la différence entre la régression linéaire simple et la régression linéaire multiple ?

    La régression linéaire simple a une seule variable indépendante, tandis que la régression linéaire multiple a plusieurs variables indépendantes.
  • Qu'est-ce que le coefficient de détermination (R²) et comment l'interpréter ?

    Le coefficient de détermination (R²) mesure la proportion de la variance de la variable dépendante qui est expliquée par le modèle. Une valeur proche de 1 indique un bon ajustement du modèle aux données.
  • Comment évaluer si un modèle de régression linéaire est bon ?

    Pour évaluer un modèle de régression linéaire, vous pouvez examiner le coefficient de détermination (R²), l'erreur quadratique moyenne (EQM), les tests de signification des coefficients et l'analyse des résidus.