Mathématiques > Géométrie > Géométrie Plane > Milieu d'un segment

Le Milieu d'un Segment : Comprendre et Calculer

Découvrez la définition du milieu d'un segment, sa formule de calcul dans un repère orthonormé, et des exemples concrets pour maîtriser cette notion essentielle en géométrie plane au lycée.

Définition du Milieu d'un Segment

Le milieu d'un segment est le point de ce segment qui est situé à égale distance de ses extrémités. Autrement dit, si I est le milieu du segment [AB], alors AI = IB. Ce point partage le segment en deux segments de même longueur.

Formule du Milieu dans un Repère Orthonormé

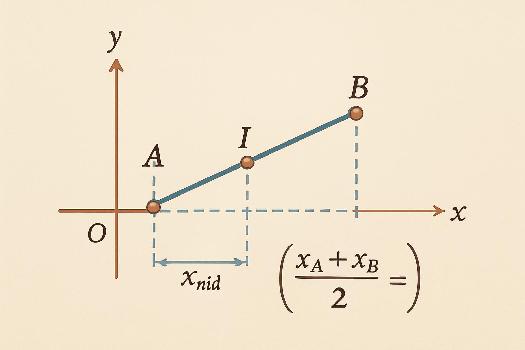
Dans un repère orthonormé (O, i, j), on peut calculer les coordonnées du milieu d'un segment [AB] à partir des coordonnées de ses extrémités.

Soient A(xA ; yA) et B(xB ; yB) les coordonnées des points A et B respectivement. Alors, les coordonnées du milieu I(xI ; yI) du segment [AB] sont données par les formules suivantes:

  • xI = (xA + xB) / 2
  • yI = (yA + yB) / 2

Explication : L'abscisse du milieu est la moyenne des abscisses des extrémités, et l'ordonnée du milieu est la moyenne des ordonnées des extrémités.

Exemple 1 : Calcul des Coordonnées du Milieu

Soient A(1 ; 3) et B(5 ; 7) deux points dans un repère orthonormé. Calculons les coordonnées du milieu I du segment [AB].

Application des formules:

  • xI = (1 + 5) / 2 = 3
  • yI = (3 + 7) / 2 = 5

Donc, les coordonnées du milieu I sont (3 ; 5).

Exemple 2 : Trouver une Extrémité Connaissant le Milieu et l'Autre Extrémité

Soit I(2 ; 4) le milieu du segment [AB], et soit A(0 ; 1). Trouver les coordonnées du point B.

Nous savons que:

  • xI = (xA + xB) / 2 => xB = 2xI - xA
  • yI = (yA + yB) / 2 => yB = 2yI - yA

Application numérique:
  • xB = 2 * 2 - 0 = 4
  • yB = 2 * 4 - 1 = 7

Donc, les coordonnées du point B sont (4 ; 7).

Propriétés Utiles

  • Le milieu d'un segment est unique.
  • La droite passant par les milieux de deux côtés d'un triangle est parallèle au troisième côté (théorème des milieux).
  • Dans un parallélogramme, les diagonales se coupent en leur milieu.

Ce qu'il faut retenir

  • Le milieu d'un segment est le point situé à égale distance des extrémités.
  • Dans un repère orthonormé, les coordonnées du milieu I(xI ; yI) du segment [AB] avec A(xA ; yA) et B(xB ; yB) sont : xI = (xA + xB) / 2 et yI = (yA + yB) / 2.
  • Connaissant le milieu et une extrémité, on peut retrouver l'autre extrémité.

← Le Cercle Trigonométrique: Découverte et Applications Le Produit Scalaire : Guide Complet pour le Lycée →

FAQ

  • Comment vérifier si un point est bien le milieu d'un segment ?

    Calculez les coordonnées du milieu du segment en utilisant la formule. Si ces coordonnées correspondent à celles du point donné, alors ce point est bien le milieu du segment. Vous pouvez aussi calculer les distances AI et IB et vérifier qu'elles sont égales.
  • Peut-on utiliser cette formule dans un repère non orthonormé ?

    Non, la formule simple que nous avons vue est valable uniquement dans un repère orthonormé. Dans un repère non orthonormé, le calcul des coordonnées du milieu est plus complexe.
  • Où utilise-t-on la notion de milieu d'un segment en dehors des exercices ?

    La notion de milieu est fondamentale dans de nombreux domaines. En géométrie, elle est utilisée dans la construction de figures et la démonstration de propriétés. Elle intervient également en physique, par exemple pour déterminer le centre de gravité d'un objet symétrique. En statistiques, la moyenne est une notion analogue au milieu.