Mathématiques > Algèbre > Équations et Inéquations > Inéquations du second degré

Utilisation du Tableau de Signe pour les Inéquations du Second Degré

Maîtrisez l'outil essentiel du tableau de signe pour résoudre facilement les inéquations du second degré. Cet article vous guide pas à pas dans la construction et l'interprétation du tableau de signe, avec des exemples concrets pour une compréhension parfaite.

Qu'est-ce qu'un Tableau de Signe ?

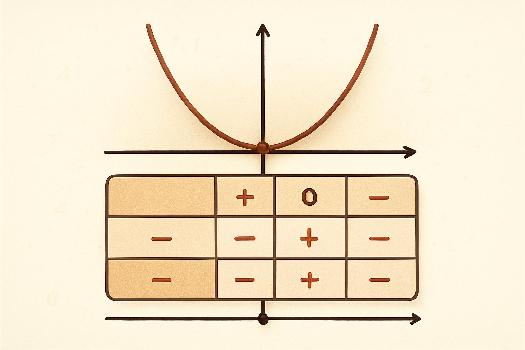
Un tableau de signe est un outil visuel qui permet d'étudier le signe d'une expression mathématique (ici, un trinôme du second degré) sur différents intervalles. Il est particulièrement utile pour résoudre les inéquations car il permet de déterminer rapidement où l'expression est positive, négative ou nulle.

Le tableau de signe se compose généralement de plusieurs lignes:

  • Une ligne pour les valeurs de x (l'axe des abscisses).
  • Une ligne pour chaque facteur de l'expression (si l'expression est factorisée).
  • Une ligne pour le signe de l'expression complète.

Construction du Tableau de Signe

La construction d'un tableau de signe pour une inéquation du second degré suit les étapes suivantes:

1. Trouver les racines: Résoudre l'équation ax2 + bx + c = 0 pour trouver les racines x1 et x2 (si elles existent).
2. Placer les racines sur la ligne des x: Ordonner les racines de la plus petite à la plus grande sur la ligne des x. Ces racines divisent la ligne des x en intervalles.
3. Déterminer le signe de chaque facteur: Si l'expression est factorisée sous la forme a(x - x1)(x - x2), déterminer le signe de chaque facteur (x - x1) et (x - x2) sur chaque intervalle. Par exemple, (x - x1) est négatif pour x < x1 et positif pour x > x1.
4. Déterminer le signe de l'expression complète: Le signe de l'expression complète est obtenu en multipliant les signes de chaque facteur sur chaque intervalle. Rappelez-vous que (+)(+) = +, (+)(-) = -, (-)(-) = +.

Interprétation du Tableau de Signe

Une fois le tableau de signe construit, il est facile de lire les intervalles où l'expression est positive, négative ou nulle. Il suffit de regarder la ligne du signe de l'expression complète et d'identifier les intervalles qui correspondent au signe recherché pour l'inéquation.

Par exemple, si on veut résoudre l'inéquation ax2 + bx + c > 0, on cherche les intervalles où le signe de l'expression est '+'. Si on veut résoudre l'inéquation ax2 + bx + c < 0, on cherche les intervalles où le signe de l'expression est '-'.

Il faut également tenir compte des racines: si l'inégalité est stricte (> ou <), les racines sont exclues des intervalles de solutions; si l'inégalité est large (≥ ou ≤), les racines sont incluses.

Exemple Détaillé avec Tableau de Signe

Résolvons l'inéquation: -x2 + 5x - 6 ≥ 0

1. Racines: Les racines de -x2 + 5x - 6 = 0 sont x1 = 2 et x2 = 3.
2. Tableau de Signe:

x-∞23+∞
x - 2-0++
x - 3--0+
-(x-2)(x-3)-0+0-


3. Interprétation: On cherche les intervalles où -x2 + 5x - 6 ≥ 0, c'est-à-dire où le signe est '+' ou '0'. D'après le tableau de signe, la solution est x ∈ [2, 3].

Cas Particuliers: Discriminant Négatif

Si le discriminant est négatif, l'équation ax2 + bx + c = 0 n'a pas de racines réelles. Dans ce cas, le trinôme conserve le même signe sur toute la ligne des x. Le tableau de signe est alors simplifié: il n'y a qu'une seule ligne pour les x et une ligne pour le signe de l'expression. Le signe de l'expression est le même que le signe de a.

Ce qu'il faut retenir

  • Le tableau de signe est un outil visuel pour étudier le signe d'une expression.
  • Il permet de résoudre les inéquations du second degré en identifiant les intervalles où l'expression est positive, négative ou nulle.
  • La construction du tableau nécessite de trouver les racines de l'équation et de déterminer le signe de chaque facteur sur chaque intervalle.
  • L'interprétation du tableau permet de déduire les intervalles de solutions de l'inéquation.

← Transformations de Graphiques de Fonctions Équations avec Valeurs Absolues : Méthodes et Exemples →

FAQ

  • Que faire si l'expression n'est pas factorisée ?

    Si l'expression n'est pas factorisée, il faut d'abord la factoriser (si possible) ou utiliser la forme développée ax2 + bx + c pour déterminer son signe en se basant sur les racines et le signe de a. Le principe reste le même: identifier les intervalles où l'expression est positive, négative ou nulle.
  • Comment gérer les inéquations avec des quotients ?

    Pour les inéquations avec des quotients, il faut également étudier le signe du numérateur et du dénominateur séparément dans le tableau de signe. Il faut faire attention aux valeurs qui annulent le dénominateur, car elles sont exclues de l'ensemble de définition.