Mathématiques > Algèbre > Suites Numériques > Suites géométriques (définition, terme général, somme)
Suites Géométriques : Comprendre et Maîtriser
Explorez en profondeur les suites géométriques, de leur définition à la somme de leurs termes. Ce cours complet est conçu pour les lycéens et offre des explications claires, des exemples concrets et des exercices pour une maîtrise parfaite.
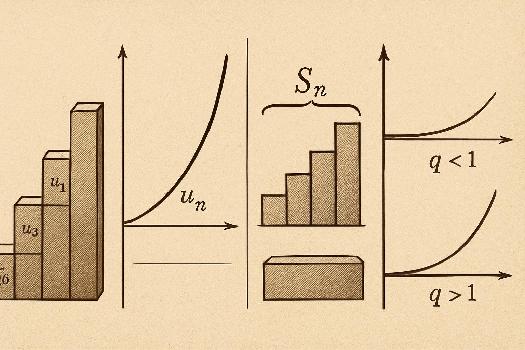
Définition d'une Suite Géométrique
Une suite est dite géométrique si, pour passer d'un terme au suivant, on multiplie toujours par le même nombre, appelé raison. En d'autres termes, le rapport entre deux termes consécutifs est constant. Mathématiquement, une suite (un) est géométrique s'il existe un nombre réel 'q' tel que, pour tout entier naturel n, un+1 = q * un. 'q' est la raison de la suite. Si q = 1, tous les termes sont égaux et la suite est constante. Si q = 0 et u0 ≠ 0, alors tous les termes, sauf le premier, sont nuls.
Exemples Concrets
- Exemple 1: La suite 2, 6, 18, 54, ... est géométrique de raison 3. Chaque terme est obtenu en multipliant le précédent par 3.
- Exemple 2: La suite 1, -2, 4, -8, 16, ... est géométrique de raison -2. La raison peut être négative, ce qui alterne le signe des termes.
- Exemple 3: La suite 5, 5, 5, 5, ... est géométrique de raison 1. C'est un cas particulier de suite géométrique constante.
Terme Général d'une Suite Géométrique
Le terme général d'une suite géométrique permet de calculer directement n'importe quel terme de la suite, sans avoir besoin de calculer les termes précédents. Si (un) est une suite géométrique de premier terme u0 et de raison q, alors son terme général est donné par : un = u0 * qn. Plus généralement, si on connaît un terme up, on peut exprimer un par : un = up * qn-p.
Démonstration du Terme Général
La formule du terme général se démontre facilement par récurrence. On a u1 = u0 * q, u2 = u1 * q = u0 * q * q = u0 * q2, u3 = u2 * q = u0 * q2 * q = u0 * q3, et ainsi de suite. On observe donc que un = u0 * qn.
Exemples d'application
- Exemple 1: Soit une suite géométrique de premier terme u0 = 3 et de raison q = 2. Quel est le 5ème terme (u4) ? Réponse : u4 = 3 * 24 = 3 * 16 = 48.
- Exemple 2: Soit une suite géométrique de deuxième terme u1 = 10 et de raison q = 0.5. Quel est le 6ème terme (u5) ? Réponse: u5 = u1 * q5-1 = 10 * 0.54 = 10 * 0.0625 = 0.625.
Somme des Termes d'une Suite Géométrique
La somme des n premiers termes d'une suite géométrique (un) de premier terme u0 et de raison q (q ≠ 1) est donnée par la formule : Sn = u0 * (1 - qn) / (1 - q). Si la somme commence à partir du terme u1, la formule devient : S'n = u1 * (1 - qn) / (1 - q). Si q = 1, la somme des n premiers termes est simplement n * u0 (ou n * u1 si la somme commence à u1).
Démonstration de la Somme des Termes
Pour démontrer cette formule, on pose Sn = u0 + u1 + ... + un-1. On multiplie ensuite chaque terme par q: q * Sn = u1 + u2 + ... + un. On soustrait ensuite la deuxième équation de la première: Sn - q * Sn = u0 - un, ce qui donne Sn * (1 - q) = u0 - u0 * qn. On divise enfin par (1 - q) pour obtenir la formule finale: Sn = u0 * (1 - qn) / (1 - q).
Exemples de calcul de somme
- Exemple 1: Soit une suite géométrique de premier terme u0 = 2 et de raison q = 3. Quelle est la somme des 4 premiers termes (S4) ? Réponse : S4 = 2 * (1 - 34) / (1 - 3) = 2 * (1 - 81) / (-2) = 2 * (-80) / (-2) = 80.
- Exemple 2: Soit une suite géométrique de premier terme u0 = 5 et de raison q = 0.5. Quelle est la somme des 5 premiers termes (S5) ? Réponse: S5 = 5 * (1 - 0.55) / (1 - 0.5) = 5 * (1 - 0.03125) / 0.5 = 5 * 0.96875 / 0.5 = 9.6875.
Limite d'une Suite Géométrique
Le comportement d'une suite géométrique lorsque n tend vers l'infini dépend de la raison q.
- Si |q| < 1 (c'est-à-dire -1 < q < 1), alors la suite converge vers 0. Cela signifie que les termes de la suite se rapprochent de plus en plus de 0 lorsque n devient très grand.
- Si q = 1, alors la suite est constante et égale à u0. Elle converge donc vers u0.
- Si q > 1, alors la suite diverge vers l'infini (positivement si u0 est positif, négativement si u0 est négatif).
- Si q < -1, alors la suite diverge et oscille entre des valeurs positives et négatives de plus en plus grandes en valeur absolue.
- Si q = -1, alors la suite oscille entre u0 et -u0 et ne converge pas.
Somme des termes d'une suite géométrique infinie
Si |q| < 1, on peut parler de la somme des termes d'une suite géométrique infinie. Cette somme, notée S∞, est donnée par: S∞ = u0 / (1 - q). Cette formule découle de la formule générale de la somme des n premiers termes en faisant tendre n vers l'infini. Puisque qn tend vers 0 lorsque n tend vers l'infini si |q| < 1, la formule Sn = u0 * (1 - qn) / (1 - q) devient S∞ = u0 / (1 - q).
Ce qu'il faut retenir
- Définition : Une suite géométrique est une suite où chaque terme est obtenu en multipliant le terme précédent par une constante, appelée raison (q).
- Terme général : un = u0 * qn (où u0 est le premier terme).
- Somme des n premiers termes (q ≠ 1) : Sn = u0 * (1 - qn) / (1 - q).
- Si q = 1 : Sn = n * u0.
- Limite si |q| < 1 : La suite converge vers 0.
- Limite si q > 1 : La suite diverge vers l'infini.
- Somme d'une suite géométrique infinie (|q| < 1) : S∞ = u0 / (1 - q).
FAQ
-
Comment identifier une suite géométrique ?
Calculez le rapport entre plusieurs paires de termes consécutifs. Si le rapport est constant, alors la suite est géométrique. Autrement dit, vérifiez que un+1 / un est constant pour différentes valeurs de n. -
Que se passe-t-il si la raison d'une suite géométrique est négative ?
Si la raison est négative, les termes de la suite alternent entre des valeurs positives et négatives. La suite n'est pas monotone. -
La formule de la somme des termes d'une suite géométrique fonctionne-t-elle toujours ?
Non, la formule Sn = u0 * (1 - qn) / (1 - q) ne fonctionne que si la raison q est différente de 1. Si q = 1, alors Sn = n * u0. -
Comment trouver la raison d'une suite géométrique ?
Divisez n'importe quel terme (sauf le premier) par le terme précédent. Par exemple, q = u1 / u0 ou q = u2 / u1, etc.
