Calcul du Déterminant d'une Matrice Carrée (2x2 et 3x3)

Introduction au Déterminant

Le déterminant d'une matrice carrée est un nombre qui encapsule certaines propriétés de la matrice, notamment son inversibilité. C'est un outil fondamental en algèbre linéaire et il a de nombreuses applications, notamment dans la résolution de systèmes d'équations linéaires et le calcul d'aires et de volumes.

Déterminant d'une matrice 2x2

Pour une matrice 2x2 de la forme :

A = | a b |
| c d |

Le déterminant, noté det(A) ou |A|, est calculé comme suit :

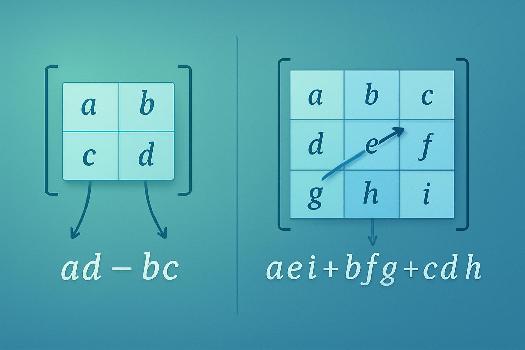
det(A) = ad - bc

Exemple :

Soit la matrice A = | 2 3 |
| 1 4 |

det(A) = (2 * 4) - (3 * 1) = 8 - 3 = 5

Déterminant d'une matrice 3x3 - Règle de Sarrus

Pour une matrice 3x3 de la forme :

A = | a b c |
| d e f |
| g h i |

On peut utiliser la règle de Sarrus pour calculer le déterminant :

det(A) = aei + bfg + cdh - ceg - bdi - afh

Pour appliquer la règle de Sarrus, on recopie les deux premières colonnes à droite de la matrice :

| a b c | a b |
| d e f | d e |
| g h i | g h |

On calcule ensuite la somme des produits des diagonales descendantes (de gauche à droite) et on soustrait la somme des produits des diagonales montantes (de gauche à droite).

Exemple :

Soit la matrice A = | 1 2 3 |
| 4 5 6 |
| 7 8 9 |

det(A) = (1 * 5 * 9) + (2 * 6 * 7) + (3 * 4 * 8) - (3 * 5 * 7) - (2 * 4 * 9) - (1 * 6 * 8)

det(A) = 45 + 84 + 96 - 105 - 72 - 48 = 0

Déterminant d'une matrice 3x3 - Développement par rapport à une ligne ou une colonne

Une autre méthode pour calculer le déterminant d'une matrice 3x3 est le développement par rapport à une ligne ou une colonne. Cette méthode est plus générale et peut être étendue à des matrices de plus grande taille.

Par exemple, en développant par rapport à la première ligne :

det(A) = a * C₁₁ + b * C₁₂ + c * C₁₃

Où C_ij est le cofacteur de l'élément a_ij, donné par :

C_ij = (-1)^i+j * M_ij

Et M_ij est le mineur de l'élément a_ij, c'est-à-dire le déterminant de la sous-matrice obtenue en supprimant la i-ème ligne et la j-ème colonne.

Exemple :

Reprenons la matrice A = | 1 2 3 |
| 4 5 6 |
| 7 8 9 |

det(A) = 1 * |5 6| - 2 * |4 6| + 3 * |4 5|
                           |8 9|                  |7 9|                  |7 8|

det(A) = 1 * (5*9 - 6*8) - 2 * (4*9 - 6*7) + 3 * (4*8 - 5*7)

det(A) = 1 * (45 - 48) - 2 * (36 - 42) + 3 * (32 - 35)

det(A) = -3 + 12 - 9 = 0

Ce qu'il faut retenir

• Le déterminant d'une matrice 2x2 | a b | est ad - bc.| c d |
• La règle de Sarrus est une méthode simple pour calculer le déterminant d'une matrice 3x3.
• Le développement par rapport à une ligne ou une colonne est une méthode plus générale pour calculer le déterminant d'une matrice 3x3, applicable aussi aux matrices de plus grande taille.
• Un déterminant nul indique que la matrice n'est pas inversible.