Exercices : Mise en Pratique de la Continuité

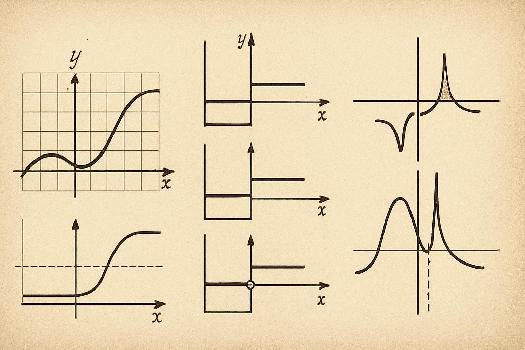
Exercice 1 : Identification de Fonctions Continues

Pour chacune des fonctions suivantes, déterminez si elle est continue sur son domaine de définition. Justifiez votre réponse en utilisant la notion intuitive de continuité (peut-on tracer le graphe sans lever le crayon ?).

1. f(x) = 2x + 3
2. g(x) = 1/(x - 2)
3. h(x) = √x (racine carrée de x)
4. k(x) = tan(x) (tangente de x)
5. l(x) = |x - 1| (valeur absolue de x - 1)

Exercice 2 : Continuité et Fonctions Définies par Morceaux

Considérez la fonction définie par morceaux suivante : f(x) = x² si x < 1 et f(x) = x + 1 si x ≥ 1.

• Est-ce que f(1) est définie ?
• Calculez la limite de f(x) quand x tend vers 1 par la gauche (lim _x→1^- f(x)).
• Calculez la limite de f(x) quand x tend vers 1 par la droite (lim _x→1⁺ f(x)).
• Est-ce que la fonction est continue en x = 1 ? Justifiez votre réponse.

Exercice 3 : Analyse de la Continuité Graphique

On vous donne le graphe d'une fonction. Examinez le graphe attentivement. Y a-t-il des points où le graphe 'saute', présente un 'trou' ou une asymptote verticale ? Identifiez ces points et expliquez pourquoi la fonction est discontinue en ces points.

Exercice 4 : Recherche des points de discontinuité

Déterminer les points de discontinuité des fonctions suivantes:

1. f(x) = (x+1) / (x-3)
2. g(x) = (x² - 4) / (x - 2)
3. h(x) = 1 / sin(x)

Exercice 5 : Construction d'une fonction discontinue

Pouvez-vous définir une fonction par morceaux qui est continue partout sauf en x = 2, où elle présente une discontinuité de type 'saut' ? Décrivez votre fonction et expliquez pourquoi elle remplit ces conditions.

Ce qu'il faut retenir

• Continuité Graphique : Visualiser le graphe d'une fonction aide à identifier les points de discontinuité.
• Fonctions par Morceaux : L'analyse de la continuité des fonctions définies par morceaux nécessite de vérifier les limites à gauche et à droite aux points de jonction.
• Points de Discontinuité : Les points de discontinuité peuvent être des sauts, des trous ou des asymptotes verticales.