Mathématiques > Probabilités et Statistiques > Probabilités > Loi binomiale (schéma de Bernoulli, probabilité)

La Loi Binomiale : Comprendre le Schéma de Bernoulli et Calculer les Probabilités

Explorez la loi binomiale, le schéma de Bernoulli et le calcul des probabilités associées. Ce guide complet, illustré d'exemples, est conçu pour les élèves de lycée.

Introduction au Schéma de Bernoulli

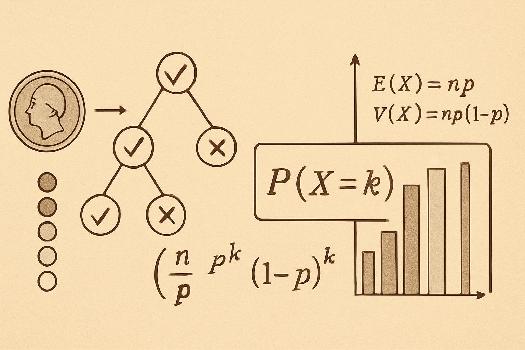
Le schéma de Bernoulli est la base de la loi binomiale. Imaginez une expérience simple avec seulement deux issues possibles : succès ou échec. Par exemple, lancer une pièce de monnaie (pile ou face) ou tester si un produit est défectueux (oui ou non). On répète cette expérience de manière indépendante un certain nombre de fois. C'est cette répétition d'expériences de Bernoulli qui forme le schéma de Bernoulli.

Plus formellement, un schéma de Bernoulli de paramètres n et p consiste à répéter n fois de manière indépendante une épreuve de Bernoulli où la probabilité de succès est p (et donc la probabilité d'échec est 1 - p).

Définition d'une Épreuve de Bernoulli

Une épreuve de Bernoulli est une expérience aléatoire qui n'a que deux issues possibles :

  • Succès (S) : l'événement qui nous intéresse
  • Échec (E) : tout autre événement qui n'est pas le succès

On note généralement p la probabilité de succès et q = 1 - p la probabilité d'échec.

Exemple Concret : Lancer de Pièce

Prenons l'exemple simple du lancer d'une pièce de monnaie équilibrée. Si on considère que 'obtenir pile' est un succès, alors :

  • La probabilité de succès (obtenir pile) est p = 0.5
  • La probabilité d'échec (obtenir face) est q = 1 - 0.5 = 0.5

Si on lance la pièce 5 fois de suite, en considérant chaque lancer comme indépendant des autres, nous avons un schéma de Bernoulli avec n = 5 et p = 0.5.

La Loi Binomiale

La loi binomiale permet de calculer la probabilité d'obtenir un nombre précis de succès lors d'un schéma de Bernoulli. Plus précisément, si on répète n fois une épreuve de Bernoulli de probabilité de succès p, la variable aléatoire X qui compte le nombre de succès suit une loi binomiale de paramètres n et p. On note cela X ~ B(n, p).

La formule pour calculer la probabilité d'obtenir exactement k succès (où k est un entier compris entre 0 et n) est la suivante :

P(X = k) = C(n, k) * pk * (1 - p)(n - k)

où C(n, k) est le coefficient binomial, qui se lit 'k parmi n' et se calcule comme :
C(n, k) = n! / (k! * (n - k)!)

avec '!' représentant la factorielle (par exemple, 5! = 5 * 4 * 3 * 2 * 1).

Coefficient Binomial : C(n, k)

Le coefficient binomial C(n, k) représente le nombre de façons différentes de choisir k éléments parmi un ensemble de n éléments, sans tenir compte de l'ordre. On peut aussi le voir comme le nombre de chemins différents pour obtenir k succès en n tentatives. La calculatrice permet de calculer directement ce coefficient avec la touche 'nCr'.

Exemple de Calcul avec la Loi Binomiale

Reprenons l'exemple du lancer de pièce. On lance la pièce 5 fois (n = 5) et on veut savoir quelle est la probabilité d'obtenir exactement 3 'pile' (k = 3). La probabilité d'obtenir 'pile' est p = 0.5.

Donc, on veut calculer P(X = 3).

1. Calcul du coefficient binomial : C(5, 3) = 5! / (3! * 2!) = (5 * 4 * 3 * 2 * 1) / ((3 * 2 * 1) * (2 * 1)) = 10
2. Application de la formule : P(X = 3) = 10 * (0.5)3 * (0.5)2 = 10 * 0.125 * 0.25 = 0.3125

Donc, la probabilité d'obtenir exactement 3 'pile' en 5 lancers est de 0.3125, soit 31.25%.

Utilisation de la Calculatrice

La plupart des calculatrices scientifiques permettent de calculer directement les probabilités associées à la loi binomiale. Consultez le manuel de votre calculatrice pour connaître la procédure exacte, mais en général, vous trouverez des fonctions comme 'binompdf' (pour calculer P(X = k)) et 'binomcdf' (pour calculer P(X ≤ k)). Pour notre exemple, binompdf(5, 0.5, 3) donnerait directement 0.3125.

Espérance et Variance de la Loi Binomiale

Si X suit une loi binomiale B(n, p), alors :

  • L'espérance (la valeur moyenne que l'on s'attend à obtenir) est E(X) = n * p
  • La variance (une mesure de la dispersion des résultats) est V(X) = n * p * (1 - p)

Dans notre exemple du lancer de pièce (n = 5, p = 0.5) :
  • E(X) = 5 * 0.5 = 2.5 (en moyenne, on s'attend à obtenir 2.5 'pile')
  • V(X) = 5 * 0.5 * 0.5 = 1.25

Ce qu'il faut retenir

  • Schéma de Bernoulli : Répétition de manière indépendante d'une épreuve avec deux issues (succès/échec).
  • Épreuve de Bernoulli : Expérience aléatoire avec seulement deux issues possibles.
  • Loi Binomiale B(n, p) : Modélise le nombre de succès lors de n répétitions d'une épreuve de Bernoulli de probabilité de succès p.
  • Formule : P(X = k) = C(n, k) * pk * (1 - p)(n - k)
  • Coefficient Binomial C(n, k) : Nombre de façons de choisir k éléments parmi n.
  • Espérance : E(X) = n * p
  • Variance : V(X) = n * p * (1 - p)

← Indépendance d'événements : Cours complet et exemples Loi de probabilité discrète →

FAQ

  • Quelle est la différence entre un schéma de Bernoulli et une loi binomiale ?

    Le schéma de Bernoulli est la répétition d'épreuves indépendantes, chacune ayant deux issues. La loi binomiale modélise le *nombre* de succès dans ce schéma.
  • Comment savoir si on peut utiliser la loi binomiale ?

    Il faut que les épreuves soient indépendantes, qu'il n'y ait que deux issues possibles à chaque épreuve, et que la probabilité de succès soit la même à chaque épreuve.
  • Comment utiliser la calculatrice pour calculer les probabilités binomiales ?

    La plupart des calculatrices ont des fonctions `binompdf` pour P(X=k) et `binomcdf` pour P(X≤k). Consultez le manuel de votre calculatrice pour plus d'informations.