Mathématiques > Algèbre > Équations et Inéquations > Systèmes d'équations linéaires

Résolution de Systèmes d'Équations Linéaires par Substitution

Apprenez à résoudre des systèmes d'équations linéaires par la méthode de substitution. Comprenez chaque étape avec des exemples détaillés.

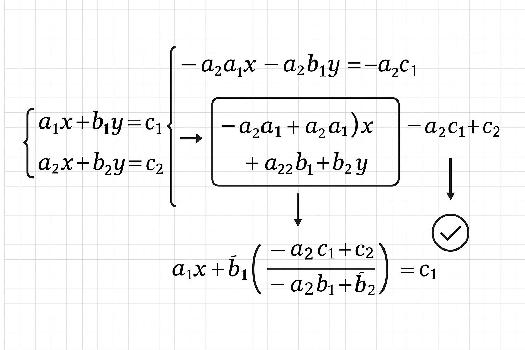
Introduction aux Systèmes d'Équations Linéaires

Un système d'équations linéaires est un ensemble d'équations linéaires impliquant les mêmes variables. Résoudre un tel système signifie trouver les valeurs de ces variables qui satisfont toutes les équations simultanément. Imaginez que vous avez deux équations qui représentent des lignes droites sur un graphique. La solution du système est le point où ces lignes se croisent (si elles se croisent). Nous allons explorer la méthode de substitution, une technique puissante pour trouver cette solution.

La Méthode de Substitution: Étape par Étape

La méthode de substitution consiste à isoler une variable dans l'une des équations, puis à substituer cette expression dans les autres équations. Voici les étapes détaillées:

  1. Isoler une variable: Choisissez l'une des équations et isolez une des variables (par exemple, exprimez 'x' en fonction de 'y', ou vice versa). Cherchez l'équation où une variable a un coefficient de 1, car cela simplifiera l'isolation.
  2. Substituer: Remplacez la variable isolée dans l'autre équation par l'expression que vous avez obtenue. Cela vous donnera une équation avec une seule variable.
  3. Résoudre l'équation: Résolvez l'équation à une seule variable pour trouver sa valeur.
  4. Substituer à nouveau: Remplacez la valeur que vous avez trouvée dans l'expression de la variable isolée (étape 1) pour trouver la valeur de l'autre variable.
  5. Vérifier: Vérifiez vos solutions en les substituant dans les équations originales. Elles doivent satisfaire toutes les équations du système.

Exemple 1: Système Simple

Considérons le système suivant: x + y = 5 x - y = 1

  1. Isoler 'x' dans la première équation: x = 5 - y
  2. Substituer 'x' dans la deuxième équation: (5 - y) - y = 1
  3. Résoudre pour 'y': 5 - 2y = 1 => -2y = -4 => y = 2
  4. Substituer 'y' dans l'expression de 'x': x = 5 - 2 => x = 3
  5. Vérifier: 3 + 2 = 5 (Vrai) et 3 - 2 = 1 (Vrai). Donc, la solution est x = 3 et y = 2.

Exemple 2: Système un peu plus complexe

Considérons le système suivant: 2x + y = 7 x + 3y = 4

  1. Isoler 'x' dans la deuxième équation: x = 4 - 3y
  2. Substituer 'x' dans la première équation: 2(4 - 3y) + y = 7
  3. Résoudre pour 'y': 8 - 6y + y = 7 => -5y = -1 => y = 1/5
  4. Substituer 'y' dans l'expression de 'x': x = 4 - 3(1/5) => x = 4 - 3/5 = 17/5
  5. Vérifier: 2(17/5) + 1/5 = 34/5 + 1/5 = 35/5 = 7 (Vrai) et 17/5 + 3(1/5) = 17/5 + 3/5 = 20/5 = 4 (Vrai). Donc, la solution est x = 17/5 et y = 1/5.

Cas Particuliers

Parfois, en appliquant la méthode de substitution, on peut rencontrer deux situations particulières :

  • Aucune solution : Si la substitution conduit à une contradiction (par exemple, 0 = 1), cela signifie que le système n'a pas de solution. Les droites représentées par les équations sont parallèles et ne se croisent jamais.
  • Infinité de solutions : Si la substitution conduit à une identité (par exemple, 0 = 0), cela signifie que le système a une infinité de solutions. Les droites représentées par les équations sont confondues, c'est-à-dire qu'elles représentent la même droite.

Ce qu'il faut retenir

  • Définition : Un système d'équations linéaires est un ensemble d'équations linéaires avec les mêmes variables.
  • Méthode de substitution : Isoler une variable dans une équation, puis substituer son expression dans l'autre équation.
  • Étapes clés : Isoler, substituer, résoudre, substituer à nouveau, vérifier.
  • Cas particuliers : Absence de solution (contradiction) ou infinité de solutions (identité).

← Résolution de Systèmes d'Équations Linéaires par Combinaison Linéaire (Élimination) Résolution graphique d'équations et d'inéquations : Une approche visuelle →

FAQ

  • Quand est-il préférable d'utiliser la méthode de substitution plutôt que la méthode d'élimination ?

    La méthode de substitution est particulièrement utile lorsque l'une des équations a déjà une variable isolée, ou lorsqu'il est facile d'isoler une variable. La méthode d'élimination peut être plus efficace lorsque les coefficients des variables sont simples à manipuler pour les annuler.
  • Que faire si, après substitution, je me retrouve avec une équation sans variable ?

    Si vous obtenez une égalité toujours vraie (par exemple, 0 = 0), le système a une infinité de solutions. Si vous obtenez une égalité fausse (par exemple, 0 = 1), le système n'a pas de solution.