Mathématiques > Analyse > Fonctions Exponentielle et Logarithme > Fonction exponentielle (définition, propriétés, courbe)

Fonction Exponentielle : Une Exploration Complète

Découvrez la fonction exponentielle, ses propriétés fondamentales, sa représentation graphique et ses applications. Un guide détaillé pour les élèves de lycée.

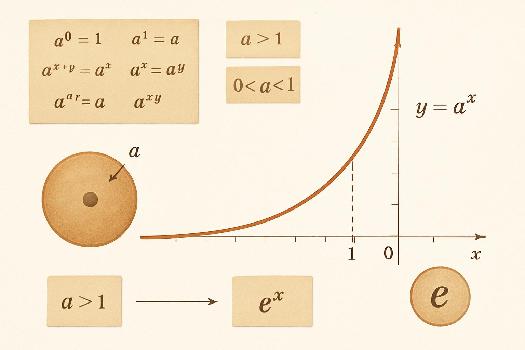
Définition de la Fonction Exponentielle

La fonction exponentielle, notée généralement f(x) = ax, où 'a' est un nombre réel positif différent de 1 (a > 0 et a ≠ 1), est une fonction fondamentale en mathématiques. Le nombre 'a' est appelé la base de la fonction exponentielle.

Cas Particulier : La fonction exponentielle naturelle, notée ex, est un cas particulier où la base 'a' est le nombre d'Euler (e ≈ 2.71828). Elle est extrêmement importante en analyse et apparaît dans de nombreux contextes mathématiques et scientifiques. On la note souvent exp(x).

Propriétés Fondamentales

La fonction exponentielle possède plusieurs propriétés importantes :

  • a0 = 1 : Pour toute base 'a', la fonction exponentielle évaluée en 0 est égale à 1. Ceci est dû au fait que tout nombre non nul élevé à la puissance 0 est égal à 1.
  • a1 = a : La fonction exponentielle évaluée en 1 est égale à la base 'a'.
  • ax+y = ax * ay : La fonction exponentielle transforme les sommes en produits. C'est une propriété très utile pour simplifier les expressions.
  • ax-y = ax / ay : La fonction exponentielle transforme les différences en quotients.
  • (ax)y = axy : Lorsque l'on élève une puissance à une autre puissance, on multiplie les exposants.
  • Si a > 1, la fonction est strictement croissante : Lorsque x augmente, ax augmente également.
  • Si 0 < a < 1, la fonction est strictement décroissante : Lorsque x augmente, ax diminue.

Exemples :
  • 23 * 22 = 23+2 = 25 = 32
  • (32)3 = 32*3 = 36 = 729

Représentation Graphique

La représentation graphique de la fonction exponentielle a une forme caractéristique. Elle passe toujours par le point (0, 1).

Cas a > 1 : La courbe croît de manière exponentielle, tendant vers l'infini lorsque x tend vers l'infini, et s'approche de 0 lorsque x tend vers moins l'infini.

Cas 0 < a < 1 : La courbe décroît de manière exponentielle, tendant vers l'infini lorsque x tend vers moins l'infini, et s'approche de 0 lorsque x tend vers l'infini.

Fonction exponentielle naturelle (ex) : C'est une fonction croissante dont la pente augmente constamment. Elle est particulièrement importante car sa dérivée est elle-même.

Applications

La fonction exponentielle a de nombreuses applications dans divers domaines :

  • Croissance et Décroissance : Modélisation de la croissance d'une population, la désintégration radioactive, etc.
  • Finance : Calcul des intérêts composés.
  • Physique : Décrit de nombreux phénomènes comme la décharge d'un condensateur.

Ce qu'il faut retenir

  • La fonction exponentielle est définie par f(x) = ax, où a > 0 et a ≠ 1.
  • a0 = 1 et a1 = a.
  • ax+y = ax * ay et ax-y = ax / ay.
  • (ax)y = axy.
  • Si a > 1, la fonction est croissante ; si 0 < a < 1, elle est décroissante.
  • La courbe passe toujours par le point (0, 1).
  • La fonction exponentielle naturelle est ex.

← Fonction Dérivée : Définition, Calcul et Applications Guide Complet des Dérivées de Fonctions Usuelles →

FAQ

  • Quelle est la différence entre ax et xa ?

    Dans ax, la base est constante et l'exposant est la variable. C'est une fonction exponentielle. Dans xa, l'exposant est constant et la base est la variable. C'est une fonction puissance.
  • Pourquoi a doit-il être positif dans la fonction exponentielle ?

    Si a était négatif, ax pourrait être un nombre complexe pour certaines valeurs de x (par exemple, (-1)1/2 = i). Pour éviter cela et pour assurer que la fonction est bien définie pour tous les nombres réels x, a doit être positif.
  • Pourquoi a ne peut-il pas être égal à 1 ?

    Si a = 1, alors ax = 1x = 1 pour tout x. La fonction deviendrait une fonction constante, et elle n'aurait plus les propriétés caractéristiques d'une fonction exponentielle (croissance ou décroissance).