Mathématiques > Géométrie > Trigonométrie > Angles orientés et mesure en radians

Angles Orientés et Mesure en Radians : Un Guide Complet

Explorez le monde des angles orientés et de la mesure en radians. Ce guide détaillé, conçu pour les lycéens, vous offre une explication approfondie des concepts fondamentaux, des exemples concrets et des exercices pratiques pour maîtriser ce chapitre essentiel de la trigonométrie.

Étude des figures planes et spatiales par le calcul, les vecteurs et les transformations géométriques
Angles Orientés et Mesure en Radians : Un Guide Complet

Introduction aux Angles Orientés

Les angles que vous connaissez depuis le collège sont des angles géométriques, définis par leur mesure positive entre 0° et 180° (ou 0 et π radians). Un angle orienté, en revanche, a une orientation (un sens de rotation) et peut prendre des valeurs positives ou négatives. On parle d'angle orienté (u,v) où u et v sont deux vecteurs non nuls.

  1. Sens direct (trigonométrique) : Rotation dans le sens inverse des aiguilles d'une montre. Conventionnellement positif.
  2. Sens indirect (horaire) : Rotation dans le sens des aiguilles d'une montre. Conventionnellement négatif.
La mesure d'un angle orienté n'est pas unique. Si θ est une mesure d'un angle orienté, alors θ + 2kπ (où k est un entier relatif) est également une mesure du même angle. C'est pourquoi on parle de *mesure modulo 2π*. On utilise souvent l'expression « une mesure de l'angle » plutôt que « la mesure de l'angle ».

Le Cercle Trigonométrique

Le cercle trigonométrique est un cercle de rayon 1, centré à l'origine d'un repère orthonormé. Il est crucial pour comprendre les angles orientés et les radians.

  1. Placement des angles : Pour placer un angle orienté θ sur le cercle trigonométrique, on part du point (1,0) et on se déplace sur le cercle dans le sens direct si θ est positif, et dans le sens indirect si θ est négatif. La longueur de l'arc parcouru est égale à la valeur absolue de θ si θ est mesuré en radians.
  2. Coordonnées d'un point : Les coordonnées du point sur le cercle trigonométrique correspondant à l'angle θ sont (cos θ, sin θ). Ceci relie directement les angles orientés aux fonctions trigonométriques.
Par exemple, pour un angle de π/2 radians (90°), le point correspondant sur le cercle trigonométrique est (0,1). Pour un angle de π radians (180°), le point est (-1,0).

Mesure en Radians

La mesure en radians est une autre façon de mesurer les angles, et elle est particulièrement utile en mathématiques avancées et en physique. Un radian est défini comme l'angle au centre d'un cercle qui intercepte un arc de longueur égale au rayon du cercle.

  • Conversion degrés-radians : Pour convertir des degrés en radians, multipliez par π/180. Pour convertir des radians en degrés, multipliez par 180/π.
  • Angle complet : Un cercle complet (360°) correspond à 2π radians. Un demi-cercle (180°) correspond à π radians.
Voici quelques exemples de conversion :
Angle en degrés Angle en radians
0° 0 radians
30° π/6 radians
45° π/4 radians
60° π/3 radians
90° π/2 radians
180° π radians
360° 2π radians

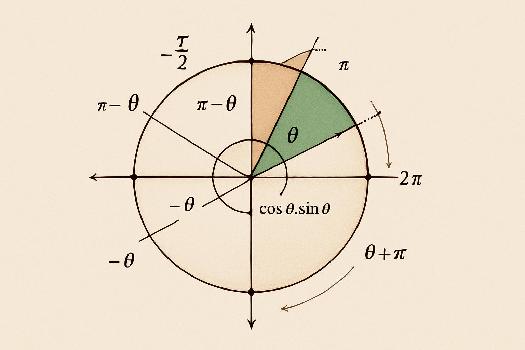
Angles Associés

Les angles associés sont des angles qui ont des relations spécifiques entre eux et permettent de simplifier les calculs trigonométriques.

  • Angles opposés (-θ) : cos(-θ) = cos(θ) et sin(-θ) = -sin(θ)
  • Angles supplémentaires (π - θ) : cos(π - θ) = -cos(θ) et sin(π - θ) = sin(θ)
  • Angles complémentaires (π/2 - θ) : cos(π/2 - θ) = sin(θ) et sin(π/2 - θ) = cos(θ)
  • Angles θ + π : cos(θ + π) = -cos(θ) et sin(θ + π) = -sin(θ)
Comprendre ces relations est essentiel pour résoudre des équations trigonométriques et simplifier des expressions.

Applications des Angles Orientés et Radians

Les angles orientés et les radians sont utilisés dans de nombreux domaines :

  • Physique : Mouvement circulaire, ondes, optique.
  • Ingénierie : Conception de structures, navigation.
  • Informatique : Graphismes, jeux vidéo.
Un exemple concret est le mouvement d'un pendule. L'angle que fait le pendule avec la verticale peut être exprimé en radians, et sa variation au cours du temps décrit un mouvement oscillatoire. Les angles orientés et la mesure en radians sont également utilisés pour décrire la rotation des roues d'une voiture, ou le mouvement des planètes autour du soleil.

Ce qu'il faut retenir

  • Angle orienté : Angle ayant un sens (direct ou indirect). Mesure non unique (modulo 2π).
  • Cercle trigonométrique : Cercle de rayon 1 centré à l'origine. Essentiel pour visualiser les angles et leurs fonctions trigonométriques.
  • Mesure en radians : Unité de mesure d'angle où 2π radians = 360°. Conversion degrés-radians.
  • Angles associés : Relations entre les cosinus et sinus d'angles tels que -θ, π - θ, π/2 - θ, θ + π.
  • Applications : Physique, ingénierie, informatique.
Il est important de maîtriser les conversions degrés-radians et de bien comprendre le cercle trigonométrique pour manipuler les angles orientés avec aisance.

← Fonctions Trigonométriques Réciproques dans le Triangle Rectangle Exercices Corrigés : Maîtriser les Angles Orientés et les Radians →

FAQ

  • Quelle est la différence entre un angle géométrique et un angle orienté ?

    Un angle géométrique est toujours positif et compris entre 0° et 180°. Un angle orienté a un sens (positif ou négatif) et peut prendre n'importe quelle valeur réelle.
  • Comment convertir des degrés en radians ?

    Pour convertir des degrés en radians, multipliez par π/180.
  • Pourquoi utilise-t-on les radians en mathématiques avancées ?

    Les radians simplifient de nombreuses formules en calcul et en trigonométrie. Ils sont également l'unité naturelle pour exprimer les angles dans le contexte des fonctions trigonométriques.
  • Comment trouver tous les angles qui ont le même sinus ?

    Si sin(θ) = sin(α), alors θ = α + 2kπ ou θ = π - α + 2kπ, où k est un entier relatif.