Mathématiques > Algèbre > Polynômes > Signe d'un polynôme du second degré
Étude du Signe d'un Polynôme du Second Degré
Apprenez à déterminer le signe d'un polynôme du second degré en fonction de son discriminant et de son coefficient dominant. Ce cours détaillé, illustré d'exemples, est parfait pour les lycéens.
Définition d'un Polynôme du Second Degré
Un polynôme du second degré (ou trinôme) est une expression de la forme ax2 + bx + c, où a, b, et c sont des nombres réels, et a est différent de zéro (a ≠ 0). L'étude du signe de ce polynôme consiste à déterminer pour quelles valeurs de x, le polynôme est positif, négatif ou nul.
Le Discriminant (Δ)
Le discriminant, noté Δ (delta), est une valeur cruciale pour étudier le signe du polynôme. Il est défini par la formule : Δ = b2 - 4ac. La valeur de Δ influence directement le nombre de racines (solutions) de l'équation ax2 + bx + c = 0.
Les Différents Cas Selon la Valeur de Δ
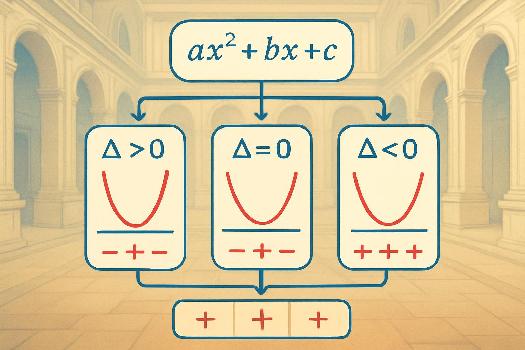
Voici les trois cas possibles :
- Cas 1: Δ > 0. Le polynôme a deux racines réelles distinctes, que l'on note généralement x1 et x2. Dans ce cas, le polynôme change de signe entre les racines.
- Cas 2: Δ = 0. Le polynôme a une seule racine réelle (on dit une racine double), que l'on note x0. Le polynôme a toujours le même signe (celui de a), sauf en x0 où il s'annule.
- Cas 3: Δ < 0. Le polynôme n'a pas de racine réelle. Il a toujours le même signe, celui de a, pour toutes les valeurs de x.
Tableau de Signe
Le tableau de signe est un outil essentiel pour visualiser le signe du polynôme. Il se construit en plaçant les racines (s'il y en a) sur une ligne, et en indiquant le signe du polynôme dans les intervalles définis par ces racines. La règle générale est la suivante:
- Si a > 0 (coefficient dominant positif) : le polynôme est positif à l'extérieur des racines (si elles existent) et négatif entre les racines.
- Si a < 0 (coefficient dominant négatif) : le polynôme est négatif à l'extérieur des racines (si elles existent) et positif entre les racines.
Exemple 1: x2 - 5x + 6
Considérons le polynôme x2 - 5x + 6. Ici, a = 1, b = -5, et c = 6. Calculons le discriminant: Δ = (-5)2 - 4 * 1 * 6 = 25 - 24 = 1. Puisque Δ > 0, il y a deux racines réelles distinctes. Calculons les racines: x1 = (5 - √1) / 2 = 2 et x2 = (5 + √1) / 2 = 3. Puisque a = 1 > 0, le polynôme est positif pour x < 2 et x > 3, et négatif pour 2 < x < 3. Tableau de signe:
| x | -∞ | 2 | 3 | +∞ | |
|---|---|---|---|---|---|
| x2 - 5x + 6 | + | 0 | - | 0 | + |
Exemple 2: -2x2 + 8x - 8
Considérons le polynôme -2x2 + 8x - 8. Ici, a = -2, b = 8, et c = -8. Calculons le discriminant: Δ = 82 - 4 * (-2) * (-8) = 64 - 64 = 0. Puisque Δ = 0, il y a une seule racine réelle. Calculons la racine: x0 = -8 / (2 * -2) = 2. Puisque a = -2 < 0, le polynôme est négatif pour toutes les valeurs de x sauf en x = 2 où il est nul. Tableau de signe:
| x | -∞ | 2 | +∞ |
|---|---|---|---|
| -2x2 + 8x - 8 | - | 0 | - |
Exemple 3: x2 + x + 1
Considérons le polynôme x2 + x + 1. Ici, a = 1, b = 1, et c = 1. Calculons le discriminant: Δ = 12 - 4 * 1 * 1 = 1 - 4 = -3. Puisque Δ < 0, il n'y a pas de racine réelle. Puisque a = 1 > 0, le polynôme est positif pour toutes les valeurs de x. Tableau de signe:
| x | -∞ | +∞ |
|---|---|---|
| x2 + x + 1 | + |
Ce qu'il faut retenir
- Un polynôme du second degré est de la forme ax2 + bx + c, où a ≠ 0.
- Le discriminant Δ = b2 - 4ac détermine le nombre de racines du polynôme.
- Si Δ > 0, deux racines réelles distinctes. Le polynôme change de signe entre les racines.
- Si Δ = 0, une racine réelle (double). Le polynôme a toujours le même signe (celui de a) sauf en la racine où il s'annule.
- Si Δ < 0, pas de racine réelle. Le polynôme a toujours le même signe (celui de a).
- Le tableau de signe permet de visualiser le signe du polynôme en fonction de x.
FAQ
-
Comment savoir si un polynôme du second degré est toujours positif ?
Un polynôme du second degré est toujours positif si son coefficient dominant (a) est positif et son discriminant (Δ) est négatif. -
Que faire si le discriminant est égal à zéro ?
Si le discriminant est égal à zéro, le polynôme a une seule racine réelle (une racine double). Le polynôme a le signe de a sauf en cette racine où il s'annule.
