Représentation graphique des fonctions sinus et cosinus

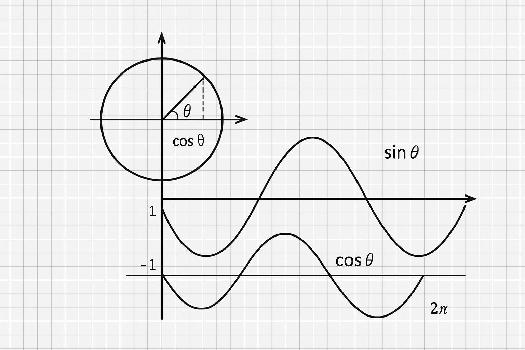
Introduction aux fonctions sinus et cosinus

Les fonctions sinus et cosinus sont des fonctions trigonométriques fondamentales qui décrivent les relations entre les angles et les côtés d'un triangle rectangle. Elles sont omniprésentes en mathématiques, en physique et dans de nombreuses autres disciplines scientifiques et techniques. Comprendre leur représentation graphique est essentiel pour visualiser et analyser leur comportement.

Ces fonctions sont définies à partir du cercle trigonométrique, un cercle de rayon 1 centré à l'origine du plan cartésien. Pour un angle θ (thêta), le sinus de θ est l'ordonnée du point sur le cercle trigonométrique correspondant à cet angle, et le cosinus de θ est l'abscisse de ce point.

La fonction sinus : y = sin(x)

La fonction sinus, notée y = sin(x), a une allure de vague qui se répète indéfiniment. Sa principale caractéristique est sa périodicité. La période du sinus est 2π (environ 6.28), ce qui signifie que le motif de la courbe se répète tous les 2π radians.

• Amplitude : L'amplitude de sin(x) est 1, ce qui signifie que la courbe oscille entre -1 et 1.
• Zéros : La fonction sinus s'annule (y = 0) aux multiples entiers de π (0, π, 2π, 3π, ...).
• Maximums : La fonction sinus atteint son maximum (y = 1) à π/2 + 2kπ, où k est un entier.
• Minimums : La fonction sinus atteint son minimum (y = -1) à 3π/2 + 2kπ, où k est un entier.

Pour tracer la courbe, vous pouvez calculer les valeurs de sin(x) pour différents angles, puis reporter ces points sur un graphique. Il est utile de connaître les valeurs de sin(x) pour les angles remarquables tels que 0, π/6, π/4, π/3, π/2, π, 3π/2 et 2π.

La fonction cosinus : y = cos(x)

La fonction cosinus, notée y = cos(x), est également une fonction périodique dont la période est 2π. Elle ressemble à la fonction sinus, mais elle est déphasée de π/2. En d'autres termes, la courbe du cosinus est la même que celle du sinus, mais décalée de π/2 unités vers la gauche.

• Amplitude : L'amplitude de cos(x) est également 1, ce qui signifie que la courbe oscille entre -1 et 1.
• Zéros : La fonction cosinus s'annule (y = 0) à π/2 + kπ, où k est un entier.
• Maximums : La fonction cosinus atteint son maximum (y = 1) à 2kπ, où k est un entier.
• Minimums : La fonction cosinus atteint son minimum (y = -1) à π + 2kπ, où k est un entier.

De même que pour le sinus, vous pouvez tracer la courbe du cosinus en calculant les valeurs de cos(x) pour différents angles et en reportant ces points sur un graphique.

Transformations des fonctions sinus et cosinus

Il est possible de transformer les fonctions sinus et cosinus en modifiant leur amplitude, leur période ou leur déphasage. Ces transformations modifient l'allure de la courbe.

• Amplitude : La fonction y = A sin(x) a une amplitude de |A|. Si A est supérieur à 1, la courbe est étirée verticalement. Si A est inférieur à 1, la courbe est comprimée verticalement. Si A est négatif, la courbe est inversée par rapport à l'axe des x.
• Période : La fonction y = sin(Bx) a une période de 2π/|B|. Si B est supérieur à 1, la période est réduite, ce qui signifie que la courbe est comprimée horizontalement. Si B est inférieur à 1, la période est augmentée, ce qui signifie que la courbe est étirée horizontalement.
• Déphasage : La fonction y = sin(x - C) est déphasée de C unités. Si C est positif, la courbe est décalée vers la droite. Si C est négatif, la courbe est décalée vers la gauche.
• Déplacement vertical : La fonction y = sin(x) + D est décalée verticalement de D unités. Si D est positif, la courbe est déplacée vers le haut. Si D est négatif, la courbe est déplacée vers le bas.

En combinant ces transformations, on peut obtenir des courbes sinus et cosinus très variées et complexes.

Exemples concrets

Voici quelques exemples de transformations des fonctions sinus et cosinus :

• y = 2sin(x) : Amplitude doublée. La courbe oscille entre -2 et 2.
• y = sin(2x) : Période divisée par 2. La courbe se répète deux fois plus vite.
• y = sin(x - π/4) : Déphasage de π/4 vers la droite.
• y = cos(x) + 1 : Déplacement vertical de 1 unité vers le haut. La courbe oscille entre 0 et 2.
• y = -sin(x) : La courbe est inversée par rapport à l'axe des x.

Ce qu'il faut retenir

• Fonctions sinus et cosinus : Définies à partir du cercle trigonométrique.
• Période : 2π pour les deux fonctions.
• Amplitude : 1 pour sin(x) et cos(x).
• Zéros : Multiples entiers de π pour sin(x), π/2 + kπ pour cos(x).
• Transformations : Modifications de l'amplitude, de la période, du déphasage et du déplacement vertical.

Comprendre ces concepts est essentiel pour analyser et interpréter les phénomènes périodiques dans de nombreux domaines scientifiques.