Mathématiques > Algèbre > Fonctions > Fonctions linéaires

Comprendre les Fonctions Linéaires

Ce cours complet explore les fonctions linéaires, de leur définition à leurs applications pratiques, avec des exemples détaillés et des exercices.

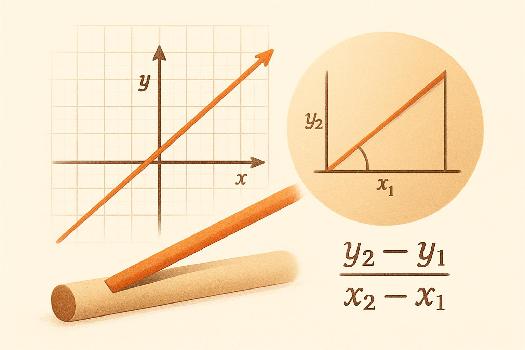
Définition d'une Fonction Linéaire

Une fonction linéaire est une fonction qui peut être représentée par une équation de la forme f(x) = ax, où a est une constante réelle appelée coefficient directeur. Le coefficient directeur a représente la pente de la droite représentant la fonction dans un repère cartésien. L'image de 0 par une fonction linéaire est toujours 0: f(0) = a * 0 = 0. C'est donc une fonction qui passe toujours par l'origine du repère.

Représentation Graphique

La représentation graphique d'une fonction linéaire est une droite passant par l'origine (0, 0). Le coefficient directeur a indique l'inclinaison de la droite. Si a est positif, la droite monte de gauche à droite. Si a est négatif, la droite descend. Pour tracer la droite, il suffit de connaître un point supplémentaire autre que (0,0). Par exemple, si f(x) = 2x, on peut prendre x = 1, ce qui donne f(1) = 2. On a donc le point (1, 2) et on peut tracer la droite reliant (0, 0) et (1, 2).

Coefficient Directeur (Pente)

Le coefficient directeur, souvent appelé pente, est crucial. Il mesure la variation de f(x) pour une variation unitaire de x. Mathématiquement, si on a deux points (x1, y1) et (x2, y2) sur la droite, alors le coefficient directeur a est donné par: a = (y2 - y1) / (x2 - x1). C'est le rapport de l'élévation (variation verticale) à la course (variation horizontale) entre deux points.

Exemples Concrets

Prenons quelques exemples pour illustrer:

  • f(x) = 3x : Pour chaque augmentation de 1 unité sur l'axe des x, la valeur de f(x) augmente de 3 unités.
  • f(x) = -2x : Pour chaque augmentation de 1 unité sur l'axe des x, la valeur de f(x) diminue de 2 unités.
  • f(x) = x : C'est la fonction identité, la droite est à 45 degrés, pour chaque augmentation de 1 unité sur l'axe des x, la valeur de f(x) augmente de 1 unité.

Déterminer l'équation d'une fonction linéaire à partir de son graphique

Pour déterminer l'équation d'une fonction linéaire à partir de son graphique, il suffit de trouver le coefficient directeur a. Comme la droite passe par l'origine, on connaît déjà un point (0, 0). Il faut donc trouver un autre point (x, y) sur la droite et utiliser la formule a = y / x. Par exemple, si la droite passe par le point (2, 6), alors a = 6 / 2 = 3, et l'équation de la fonction est f(x) = 3x.

Applications Pratiques

Les fonctions linéaires sont utilisées dans de nombreux domaines, comme:

  • La physique: pour modéliser la relation entre la distance parcourue et le temps à vitesse constante.
  • L'économie: pour modéliser la relation entre le coût total et la quantité produite.
  • La finance: pour modéliser la relation entre le taux d'intérêt et le montant des intérêts.

Ce qu'il faut retenir

  • Une fonction linéaire est de la forme f(x) = ax, où a est le coefficient directeur.
  • Sa représentation graphique est une droite passant par l'origine (0, 0).
  • Le coefficient directeur représente la pente de la droite.
  • Pour trouver le coefficient directeur, on peut utiliser la formule a = (y2 - y1) / (x2 - x1).
  • Les fonctions linéaires sont utilisées dans de nombreux domaines pour modéliser des relations linéaires.

← Comprendre l'Ensemble de Définition et l'Image d'une Fonction Comprendre les Suites Numériques : Explicites et Récurrentes →

FAQ

  • Comment savoir si une fonction est linéaire?

    Une fonction est linéaire si elle peut être écrite sous la forme f(x) = ax, où a est une constante. Sa représentation graphique est une droite passant par l'origine.
  • Quelle est la différence entre une fonction linéaire et une fonction affine?

    Une fonction linéaire est de la forme f(x) = ax, tandis qu'une fonction affine est de la forme f(x) = ax + b, où b est une constante. La fonction linéaire passe toujours par l'origine, tandis que la fonction affine non (sauf si b = 0).
  • Comment tracer le graphique d'une fonction linéaire?

    Pour tracer le graphique d'une fonction linéaire, il suffit de trouver deux points. Comme la droite passe par l'origine (0, 0), il suffit de trouver un autre point. Par exemple, si f(x) = 2x, on peut prendre x = 1, ce qui donne f(1) = 2. On a donc le point (1, 2) et on peut tracer la droite reliant (0, 0) et (1, 2).