Mathématiques > Analyse > Dérivation > Optimisation

Optimisation de fonctions : Introduction et méthodes

Ce guide complet explore l'optimisation de fonctions, une technique essentielle en analyse mathématique pour trouver les valeurs maximales et minimales d'une fonction. Nous aborderons les concepts clés, les méthodes de résolution, et des exemples concrets pour illustrer l'application de l'optimisation au niveau lycée.

Introduction à l'optimisation

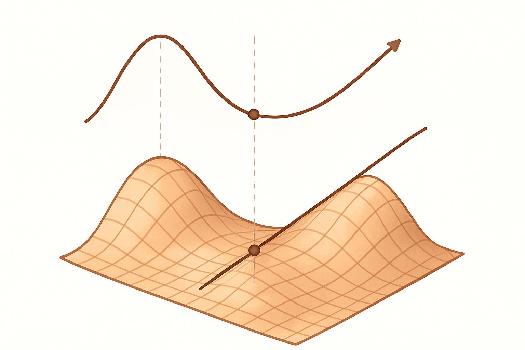
L'optimisation, en mathématiques, consiste à trouver la valeur maximale ou minimale d'une fonction sur un intervalle donné. Ces points sont appelés extrema. L'optimisation est un outil puissant avec de nombreuses applications pratiques, allant de la conception de structures solides à la maximisation des profits d'une entreprise.

Pour comprendre l'optimisation, il est crucial de maîtriser les concepts de dérivée et d'étude des variations d'une fonction. La dérivée d'une fonction donne la pente de la tangente en un point, et les points où la dérivée est nulle (ou n'existe pas) sont des candidats pour les extrema.

Conditions nécessaires et suffisantes

Condition nécessaire: Si une fonction f admet un extremum local en un point c et que f est dérivable en c, alors f'(c) = 0. Autrement dit, la dérivée de la fonction doit être nulle en un point d'extremum local (maximum ou minimum).

Condition suffisante: Si f'(c) = 0 et que f''(c) existe, alors :

  • Si f''(c) > 0, f admet un minimum local en c.
  • Si f''(c) < 0, f admet un maximum local en c.

Il est important de noter que si f''(c) = 0, on ne peut pas conclure directement sur la nature du point critique. Il faut alors étudier le signe de la dérivée première autour du point c.

Méthode générale d'optimisation

Voici les étapes clés pour optimiser une fonction f sur un intervalle [a, b]:

  1. Calculer la dérivée f'(x).
  2. Trouver les points critiques en résolvant l'équation f'(x) = 0. Ces points critiques sont les candidats pour les extrema locaux. Il faut aussi considérer les points où f'(x) n'existe pas (par exemple, les points anguleux).
  3. Étudier le signe de la dérivée f'(x) sur l'intervalle [a, b]. Ceci permet de déterminer les intervalles où f est croissante ou décroissante.
  4. Évaluer la fonction f(x) aux points critiques et aux bornes de l'intervalle (a et b).
  5. Identifier le maximum et le minimum absolus en comparant les valeurs obtenues à l'étape 4. La plus grande valeur est le maximum absolu, et la plus petite valeur est le minimum absolu.

Exemple : Trouver le maximum de la fonction f(x) = -x2 + 4x + 2 sur l'intervalle [0, 4].
  1. f'(x) = -2x + 4
  2. f'(x) = 0 => -2x + 4 = 0 => x = 2 (point critique)
  3. f'(x) > 0 pour x < 2 (f est croissante) et f'(x) < 0 pour x > 2 (f est décroissante). Donc, x = 2 est un maximum local.
  4. f(0) = 2, f(2) = 6, f(4) = 2
  5. Le maximum absolu est f(2) = 6.

Applications concrètes

L'optimisation trouve des applications dans de nombreux domaines :

  • Économie: Maximiser le profit d'une entreprise, minimiser les coûts de production.
  • Physique: Trouver la trajectoire d'un projectile qui maximise sa portée.
  • Ingénierie: Concevoir des structures qui minimisent l'utilisation de matériaux tout en respectant des contraintes de résistance.
  • Informatique: Optimiser les algorithmes pour réduire le temps d'exécution.

Exemple : Un agriculteur veut clôturer un champ rectangulaire adjacent à une rivière. Il dispose de 100 mètres de clôture. Quelles sont les dimensions du champ qui maximisent son aire, sachant qu'il n'a pas besoin de clôturer le côté le long de la rivière?
Soit x la largeur du champ et y sa longueur. La contrainte est 2x + y = 100 (périmètre). L'aire du champ est A = x * y. On veut maximiser A.
On exprime y en fonction de x : y = 100 - 2x. Donc, A(x) = x * (100 - 2x) = 100x - 2x2.
On calcule la dérivée: A'(x) = 100 - 4x. On résout A'(x) = 0 => x = 25. Donc y = 100 - 2 * 25 = 50.
La largeur optimale est 25 mètres et la longueur optimale est 50 mètres. L'aire maximale est 25 * 50 = 1250 mètres carrés.

Ce qu'il faut retenir

  • Optimisation: Recherche des extrema (maximums et minimums) d'une fonction.
  • Condition nécessaire (extremum local en c): Si f est dérivable en c, alors f'(c) = 0.
  • Condition suffisante (point critique c):
    • Si f''(c) > 0, f admet un minimum local en c.
    • Si f''(c) < 0, f admet un maximum local en c.
  • Méthode d'optimisation:
    1. Calculer f'(x).
    2. Trouver les points critiques (f'(x) = 0).
    3. Étudier le signe de f'(x).
    4. Évaluer f(x) aux points critiques et aux bornes de l'intervalle.
    5. Identifier le maximum et le minimum absolus.

← Nombre dérivé et tangente : Cours et exercices Opérations sur les limites : Addition, Soustraction, Multiplication et Division →

FAQ

  • Comment savoir si un point critique est un maximum ou un minimum?

    On peut utiliser la dérivée seconde. Si la dérivée seconde est positive en ce point, c'est un minimum. Si elle est négative, c'est un maximum. Si la dérivée seconde est nulle, il faut étudier le signe de la dérivée première autour du point critique.
  • Est-ce que tous les points où la dérivée est nulle sont des extrema?

    Non, ce sont des points critiques. Un point critique peut être un maximum local, un minimum local, ou un point d'inflexion (où la fonction change de concavité mais n'a pas d'extremum).
  • Quand est-il nécessaire d'étudier les bornes de l'intervalle?

    Il est nécessaire d'évaluer la fonction aux bornes de l'intervalle lors de la recherche des extrema absolus. Un extremum absolu peut se trouver aux bornes même si la dérivée n'y est pas nulle.