Produit matriciel : Comprendre et maîtriser le calcul matriciel

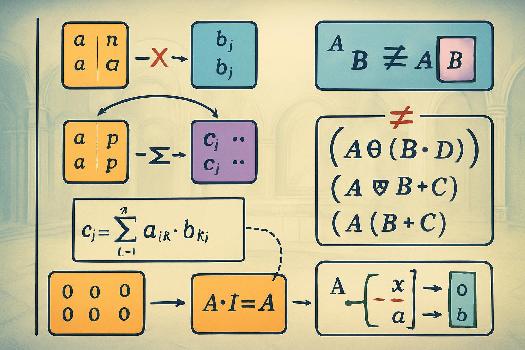
Définition du produit matriciel

Le produit matriciel est une opération qui combine deux matrices pour en produire une troisième. Contrairement à l'addition et la soustraction, le produit matriciel n'est pas aussi intuitif. Il est crucial de comprendre les dimensions des matrices impliquées. Condition de compatibilité: Pour que le produit de deux matrices A et B, noté A x B, soit possible, le nombre de colonnes de A doit être égal au nombre de lignes de B. Si A est une matrice m x n et B est une matrice n x p, alors le produit A x B est une matrice m x p.

Calcul du produit matriciel : étape par étape

Prenons deux matrices, A = (a_ij) de dimension m x n et B = (b_ij) de dimension n x p. La matrice produit C = A x B sera de dimension m x p, et chaque élément c_ij de C est calculé comme suit: cij = ai1b1j + ai2b2j + ... + ainbnj = ∑k=1n aikbkj En d'autres termes, pour trouver l'élément à la i-ème ligne et j-ème colonne de la matrice produit, on multiplie chaque élément de la i-ème ligne de A par l'élément correspondant de la j-ème colonne de B, puis on additionne tous ces produits. Exemple : Soit A = [[1, 2], [3, 4]] et B = [[5, 6], [7, 8]]. Alors A x B = C, où : c₁₁ = (1 x 5) + (2 x 7) = 5 + 14 = 19 c₁₂ = (1 x 6) + (2 x 8) = 6 + 16 = 22 c₂₁ = (3 x 5) + (4 x 7) = 15 + 28 = 43 c₂₂ = (3 x 6) + (4 x 8) = 18 + 32 = 50 Donc, C = [[19, 22], [43, 50]].

Exemple détaillé avec matrices 2x2

Illustrons le produit matriciel avec des matrices 2x2. Soient les matrices A = [[a, b], [c, d]] et B = [[e, f], [g, h]]. Alors A x B = [[ae + bg, af + bh], [ce + dg, cf + dh]]. Procédure: 1. Pour obtenir l'élément en haut à gauche de la matrice résultante (ae + bg), on multiplie la première ligne de A (a, b) par la première colonne de B (e, g) et on somme les résultats. 2. Pour l'élément en haut à droite (af + bh), on multiplie la première ligne de A (a, b) par la deuxième colonne de B (f, h) et on somme. 3. Pour l'élément en bas à gauche (ce + dg), on multiplie la deuxième ligne de A (c, d) par la première colonne de B (e, g) et on somme. 4. Pour l'élément en bas à droite (cf + dh), on multiplie la deuxième ligne de A (c, d) par la deuxième colonne de B (f, h) et on somme.

Propriétés du produit matriciel

Le produit matriciel possède des propriétés importantes à connaître : * Non-commutativité : En général, A x B ≠ B x A. C'est une différence majeure avec la multiplication des nombres réels. * Associativité : (A x B) x C = A x (B x C), à condition que les produits soient définis. * Distributivité : A x (B + C) = A x B + A x C et (A + B) x C = A x C + B x C, à condition que les sommes et produits soient définis. * Multiplication par une matrice identité : Si I est la matrice identité (une matrice carrée avec des 1 sur la diagonale principale et des 0 ailleurs), alors A x I = I x A = A, à condition que les produits soient définis. La matrice identité est l'équivalent du nombre 1 pour la multiplication matricielle. * Multiplication par un scalaire : k(A x B) = (kA) x B = A x (kB), où k est un scalaire (un nombre réel).

Cas particuliers : Matrices carrées et matrices diagonales

Matrices carrées : Le produit de deux matrices carrées de même dimension est toujours possible et donne une matrice carrée de la même dimension. Matrices diagonales : Une matrice diagonale est une matrice carrée dont tous les éléments hors de la diagonale principale sont nuls. Le produit de deux matrices diagonales est une matrice diagonale. Si A = diag(a₁, a₂, ..., a_n) et B = diag(b₁, b₂, ..., b_n), alors A x B = diag(a₁b₁, a₂b₂, ..., a_nb_n). En d'autres termes, les éléments diagonaux sont simplement multipliés.

Application : Systèmes d'équations linéaires

Le produit matriciel est un outil essentiel pour résoudre les systèmes d'équations linéaires. Un système d'équations linéaires peut être écrit sous la forme matricielle A x X = B, où A est la matrice des coefficients, X est le vecteur des inconnues et B est le vecteur des constantes. La résolution de ce système peut se faire par différentes méthodes, notamment en utilisant l'inverse de la matrice A (si elle existe).

Ce qu'il faut retenir

• Le produit matriciel A x B est défini uniquement si le nombre de colonnes de A est égal au nombre de lignes de B.
• Le produit A x B n'est généralement pas égal à B x A (non-commutativité).
• La matrice produit C = A x B a pour éléments c_ij = ∑_k=1ⁿ a_ikb_kj.
• Le produit matriciel est associatif et distributif.
• La matrice identité I vérifie A x I = I x A = A.
• Le produit matriciel est utilisé pour représenter et résoudre des systèmes d'équations linéaires (A x X = B).