Équations du second degré : Méthodes de résolution et applications

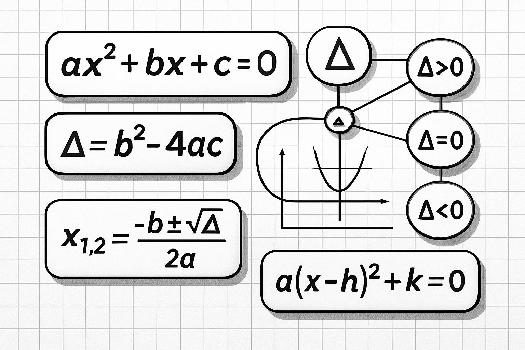
Définition d'une équation du second degré

Une équation du second degré, ou équation quadratique, est une équation polynomiale de degré deux. Sa forme générale est: ax² + bx + c = 0, où a, b, et c sont des coefficients réels, et a est non nul (sinon, l'équation deviendrait linéaire).

Exemples:

• 2x² - 5x + 3 = 0
• x² + 4x = 0
• -x² + 9 = 0

Comprendre cette forme est la première étape pour résoudre ces équations.

Méthode de factorisation

La factorisation consiste à écrire l'équation du second degré sous la forme d'un produit de deux binômes égal à zéro.

Exemple:
Soit l'équation x² - 5x + 6 = 0.
Nous cherchons deux nombres dont le produit est 6 et la somme est 5. Ces nombres sont 2 et 3.
Donc, on peut factoriser l'équation comme suit: (x - 2)(x - 3) = 0.
Pour que ce produit soit nul, il faut et il suffit que l'un des facteurs soit nul. Donc, x - 2 = 0 ou x - 3 = 0.
Les solutions sont donc x = 2 et x = 3.

La factorisation n'est pas toujours possible avec des nombres entiers, mais elle est très utile lorsqu'elle est applicable.

Utilisation du discriminant

Le discriminant, noté Δ (delta), est une expression qui permet de déterminer le nombre et la nature des solutions d'une équation du second degré. Il est calculé par la formule : Δ = b² - 4ac.

Interprétation du discriminant:

• Si Δ > 0, l'équation a deux solutions réelles distinctes.
• Si Δ = 0, l'équation a une solution réelle unique (une solution double).
• Si Δ < 0, l'équation n'a pas de solutions réelles (mais elle a deux solutions complexes).

Formule des solutions:
Si Δ ≥ 0, les solutions de l'équation ax² + bx + c = 0 sont données par :
x₁ = (-b - √Δ) / (2a) et x₂ = (-b + √Δ) / (2a).

Exemple:
Considérons l'équation 2x² + 3x - 2 = 0.
Ici, a = 2, b = 3, et c = -2.
Δ = 3² - 4 * 2 * (-2) = 9 + 16 = 25.
Comme Δ > 0, l'équation a deux solutions réelles.
x₁ = (-3 - √25) / (2 * 2) = (-3 - 5) / 4 = -2
x₂ = (-3 + √25) / (2 * 2) = (-3 + 5) / 4 = 1/2
Les solutions sont donc x = -2 et x = 1/2.

Forme canonique d'une équation du second degré

La forme canonique d'une équation du second degré permet de simplifier sa résolution. Elle s'écrit sous la forme : a(x - h)² + k = 0, où (h, k) sont les coordonnées du sommet de la parabole représentative de la fonction quadratique.

Pour transformer une équation de la forme ax² + bx + c = 0 en forme canonique, on utilise la méthode de la complétion du carré.

Étapes:

1. Factoriser a : a(x² + (b/a)x) + c = 0
2. Ajouter et soustraire (b/2a)² à l'intérieur des parenthèses : a(x² + (b/a)x + (b/2a)² - (b/2a)²) + c = 0
3. Réécrire le trinôme comme un carré : a[(x + (b/2a))² - (b/2a)²] + c = 0
4. Simplifier : a(x + (b/2a))² - a(b/2a)² + c = 0

La forme canonique est alors : a(x + (b/2a))² + (c - (b²/4a)) = 0.

Applications des équations du second degré

Les équations du second degré ont de nombreuses applications dans divers domaines tels que la physique, l'ingénierie et l'économie.

Exemples:

• Physique: Calcul de la trajectoire d'un projectile.
• Ingénierie: Conception de ponts et de structures.
• Économie: Modélisation de coûts et de revenus.

La capacité à résoudre des équations du second degré est donc essentielle pour de nombreuses professions.

Ce qu'il faut retenir

• Forme générale: ax² + bx + c = 0
• Discriminant: Δ = b² - 4ac
• Solutions:
  • Si Δ > 0: deux solutions réelles distinctes.
  • Si Δ = 0: une solution réelle unique.
  • Si Δ < 0: pas de solutions réelles.
• Formule des solutions (si Δ ≥ 0): x_1,2 = (-b ± √Δ) / (2a)
• Forme canonique: a(x - h)² + k = 0
• Méthode de factorisation: Trouver deux nombres dont le produit est c et la somme est b.