Sens de variation d'une fonction et signe de sa dérivée

Introduction

Le lien entre le sens de variation d'une fonction et le signe de sa dérivée est un pilier fondamental de l'analyse mathématique. Comprendre cette relation permet de déterminer comment une fonction évolue (croissante, décroissante ou constante) simplement en étudiant le signe de sa dérivée. Ce concept est essentiel pour l'étude des fonctions, l'optimisation et la résolution de problèmes concrets.

Définitions et Rappels

• Fonction croissante : Une fonction f est croissante sur un intervalle I si, pour tous réels a et b de I tels que a < b, on a f(a) ≤ f(b). Si f(a) < f(b), la fonction est strictement croissante.
• Fonction décroissante : Une fonction f est décroissante sur un intervalle I si, pour tous réels a et b de I tels que a < b, on a f(a) ≥ f(b). Si f(a) > f(b), la fonction est strictement décroissante.
• Fonction constante : Une fonction f est constante sur un intervalle I si, pour tout réel a et b de I, on a f(a) = f(b).
• Dérivée d'une fonction : La dérivée d'une fonction f en un point x, notée f'(x), représente le taux de variation instantané de la fonction en ce point. Géométriquement, c'est la pente de la tangente à la courbe de f au point d'abscisse x.

Théorème Fondamental

Le théorème fondamental qui relie le sens de variation et le signe de la dérivée est le suivant:

• Si f'(x) > 0 sur un intervalle I, alors la fonction f est strictement croissante sur I.
• Si f'(x) < 0 sur un intervalle I, alors la fonction f est strictement décroissante sur I.
• Si f'(x) = 0 sur un intervalle I, alors la fonction f est constante sur I.

Démonstration (Intuitive)

Pourquoi ça marche ?Imaginez une petite voiture qui se déplace sur la courbe de la fonction f.

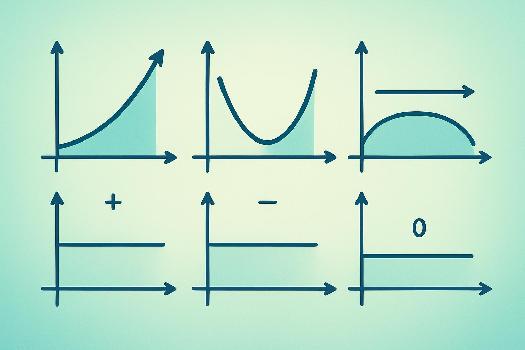
• Si la pente de la route (la dérivée) est positive, la voiture monte, donc la fonction croît.
• Si la pente de la route est négative, la voiture descend, donc la fonction décroît.
• Si la pente de la route est nulle, la route est plate, donc la fonction est constante.

Méthode pratique pour déterminer le sens de variation

1. Calculer la dérivée : Calculez la dérivée f'(x) de la fonction f(x).
2. Trouver les points critiques : Trouvez les valeurs de x pour lesquelles f'(x) = 0 ou f'(x) n'existe pas (points où la dérivée n'est pas définie). Ces points sont appelés points critiques.
3. Établir le tableau de signes de f'(x) : Construisez un tableau de signes pour f'(x) en utilisant les points critiques. Placez les points critiques sur une ligne horizontale et déterminez le signe de f'(x) dans chaque intervalle délimité par ces points. Pour cela, choisissez une valeur test dans chaque intervalle et calculez le signe de f'(x) pour cette valeur.
4. Déduire le tableau de variations de f(x) : Déduisez le sens de variation de f(x) en utilisant le théorème fondamental. Si f'(x) > 0, f(x) est croissante. Si f'(x) < 0, f(x) est décroissante. Si f'(x) = 0, f(x) est constante. Représentez le sens de variation avec des flèches dans le tableau.

Exemple 1

Soit la fonction f(x) = x² - 4x + 3.

1. Calcul de la dérivée : f'(x) = 2x - 4
2. Points critiques : f'(x) = 0 => 2x - 4 = 0 => x = 2
3. Tableau de signes de f'(x) :
   

   x	-∞	2	+∞
   f'(x)	-	0	+

4. Tableau de variations de f(x) :
   

   x	-∞	2	+∞
   f'(x)	-	0	+
   f(x)	décroissante	Minimum	croissante

   La fonction est décroissante sur ]-∞ ; 2] et croissante sur [2 ; +∞[. Elle admet un minimum en x = 2, qui vaut f(2) = -1.

Exemple 2

Soit la fonction f(x) = -x³ + 3x.

1. Calcul de la dérivée : f'(x) = -3x² + 3
2. Points critiques : f'(x) = 0 => -3x² + 3 = 0 => x² = 1 => x = -1 ou x = 1
3. Tableau de signes de f'(x) :
   

   x	-∞	-1	1	+∞
   f'(x)	-	0	+	0	-

4. Tableau de variations de f(x) :
   

   x	-∞	-1	1	+∞
   f'(x)	-	0	+	0	-
   f(x)	décroissante	Minimum	croissante	Maximum	décroissante

   La fonction est décroissante sur ]-∞ ; -1] et [1 ; +∞[ et croissante sur [-1 ; 1]. Elle admet un minimum local en x = -1, qui vaut f(-1) = -2, et un maximum local en x = 1, qui vaut f(1) = 2.

Applications

La relation entre le sens de variation et le signe de la dérivée est utilisée dans de nombreux domaines :

• Optimisation : Trouver les maximums et minimums d'une fonction.
• Modélisation : Comprendre le comportement de systèmes dynamiques.
• Économie : Analyser les coûts et les bénéfices marginaux.
• Physique : Étudier les mouvements et les forces.

Ce qu'il faut retenir

• Si f'(x) > 0 sur un intervalle I, alors la fonction f est strictement croissante sur I.
• Si f'(x) < 0 sur un intervalle I, alors la fonction f est strictement décroissante sur I.
• Si f'(x) = 0 sur un intervalle I, alors la fonction f est constante sur I.
• Pour déterminer le sens de variation d'une fonction, on calcule sa dérivée, on trouve les points critiques, on établit le tableau de signes de la dérivée, et on en déduit le tableau de variations de la fonction.