Formule de Moivre : Introduction et Applications

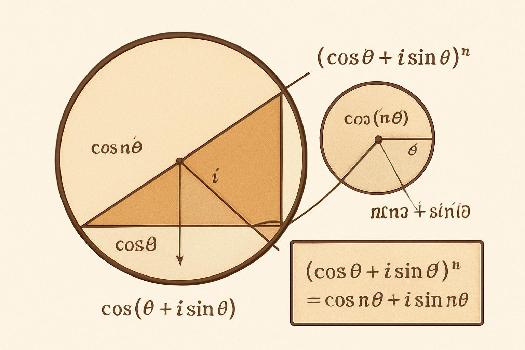
Introduction à la Formule de Moivre

La formule de Moivre est un outil fondamental en mathématiques, notamment dans l'étude des nombres complexes. Elle établit un lien direct entre les nombres complexes exprimés sous forme trigonométrique et leurs puissances. Elle simplifie grandement le calcul de puissances complexes. Pour un nombre complexe z écrit sous forme trigonométrique z = r(cos θ + i sin θ), et pour tout entier relatif n, la formule de Moivre stipule :

(cos θ + i sin θ)ⁿ = cos(nθ) + i sin(nθ)

Où :

• r est le module de z
• θ est l'argument de z
• i est l'unité imaginaire (i² = -1)

Démonstration de la Formule de Moivre

La formule de Moivre peut être démontrée par récurrence sur l'entier n.

Initialisation : Pour n = 1, la formule est trivialement vraie : (cos θ + i sin θ)¹ = cos θ + i sin θ.

Hypothèse de récurrence : Supposons que la formule soit vraie pour un certain entier k, c'est-à-dire que (cos θ + i sin θ)^k = cos(kθ) + i sin(kθ).

Étape de récurrence : Montrons que la formule est vraie pour k + 1 :

(cos θ + i sin θ)^k+1 = (cos θ + i sin θ)^k * (cos θ + i sin θ)

En utilisant l'hypothèse de récurrence :

= (cos(kθ) + i sin(kθ)) * (cos θ + i sin θ)

Développons :

= cos(kθ)cos θ - sin(kθ)sin θ + i(cos(kθ)sin θ + sin(kθ)cos θ)

En utilisant les formules trigonométriques d'addition : cos(a+b) = cos(a)cos(b) - sin(a)sin(b) et sin(a+b) = sin(a)cos(b) + cos(a)sin(b), on obtient :

= cos(kθ + θ) + i sin(kθ + θ)

= cos((k+1)θ) + i sin((k+1)θ)

Ainsi, la formule est vraie pour k + 1. Par principe de récurrence, la formule de Moivre est vraie pour tout entier naturel n. La formule peut également être étendue aux entiers négatifs.

Applications de la Formule de Moivre

La formule de Moivre possède de nombreuses applications :

• Calcul de puissances de nombres complexes : Elle permet de calculer facilement (cos θ + i sin θ)ⁿ sans avoir à effectuer la multiplication complexe n fois.
• Résolution d'équations trigonométriques : Elle peut être utilisée pour exprimer cos(nθ) et sin(nθ) en termes de cos θ et sin θ. Par exemple, on peut l'utiliser pour trouver des expressions pour cos(3θ) et sin(3θ).
• Dérivation d'identités trigonométriques : En égalant les parties réelles et imaginaires des deux côtés de la formule de Moivre, on peut dériver des identités trigonométriques.
• Calcul de racines n-ièmes de l'unité : La formule de Moivre est essentielle pour trouver les racines n-ièmes de l'unité dans le plan complexe.

Exemple 1 : Calcul de (cos(π/4) + i sin(π/4))^3

Utilisons la formule de Moivre pour calculer (cos(π/4) + i sin(π/4))³.

D'après la formule de Moivre :
(cos(π/4) + i sin(π/4))³ = cos(3 * π/4) + i sin(3 * π/4)

Calculons les valeurs :
cos(3π/4) = -√2/2
sin(3π/4) = √2/2

Donc :
(cos(π/4) + i sin(π/4))³ = -√2/2 + i √2/2

Exemple 2 : Expression de cos(3θ) en fonction de cos θ

Utilisons la formule de Moivre pour exprimer cos(3θ) en fonction de cos θ.
D'après la formule de Moivre :
(cos θ + i sin θ)³ = cos(3θ) + i sin(3θ)

Développons le membre de gauche :
(cos θ + i sin θ)³ = cos³ θ + 3i cos² θ sin θ - 3 cos θ sin² θ - i sin³ θ

Regroupons les parties réelles et imaginaires :
(cos θ + i sin θ)³ = (cos³ θ - 3 cos θ sin² θ) + i(3 cos² θ sin θ - sin³ θ)

En égalant les parties réelles, on obtient :
cos(3θ) = cos³ θ - 3 cos θ sin² θ

Utilisons l'identité sin² θ = 1 - cos² θ :
cos(3θ) = cos³ θ - 3 cos θ (1 - cos² θ)
cos(3θ) = cos³ θ - 3 cos θ + 3 cos³ θ
cos(3θ) = 4 cos³ θ - 3 cos θ

Ce qu'il faut retenir

• La formule de Moivre stipule que (cos θ + i sin θ)ⁿ = cos(nθ) + i sin(nθ) pour tout entier n.
• Elle permet de calculer des puissances de nombres complexes exprimés sous forme trigonométrique.
• Elle est utile pour dériver des identités trigonométriques et résoudre des équations trigonométriques complexes.
• Elle simplifie le calcul de racines n-ièmes de l'unité.