Mathématiques > Géométrie > Géométrie Plane > Repérage dans le plan (coordonnées cartésiennes)

Calcul de distance entre deux points dans un repère cartésien

Apprenez à calculer la distance entre deux points à partir de leurs coordonnées cartésiennes. Cette compétence fondamentale est cruciale pour résoudre divers problèmes de géométrie analytique.

La formule de la distance

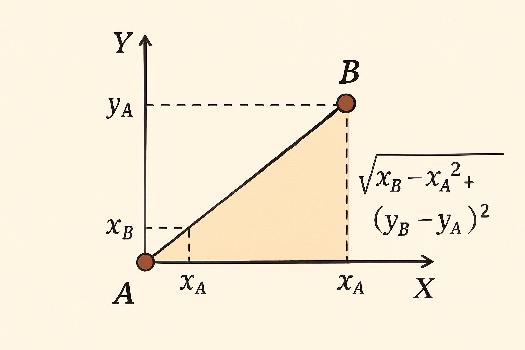
Soient deux points A(xA, yA) et B(xB, yB) dans un repère cartésien. La distance entre A et B, notée AB, est donnée par la formule suivante :

AB = √[(xB - xA)2 + (yB - yA)2]

Cette formule découle directement du théorème de Pythagore appliqué au triangle rectangle formé par les points A, B et un troisième point C de coordonnées (xB, yA). La longueur des côtés de ce triangle rectangle est |xB - xA| et |yB - yA|.

Démonstration de la formule

Considérons les points A(xA, yA) et B(xB, yB). Construisons le point C(xB, yA). Le triangle ABC est rectangle en C. Par le théorème de Pythagore, AB2 = AC2 + BC2. Or, AC = |xB - xA| et BC = |yB - yA|. Donc, AB2 = (xB - xA)2 + (yB - yA)2. En prenant la racine carrée des deux côtés, on obtient la formule de la distance.

Exemples d'application

Exemple 1 : Calculons la distance entre les points A(1, 2) et B(4, 6).
AB = √[(4 - 1)2 + (6 - 2)2] = √[32 + 42] = √(9 + 16) = √25 = 5.

Exemple 2 : Calculons la distance entre les points C(-2, 3) et D(1, -1).
CD = √[(1 - (-2))2 + (-1 - 3)2] = √[32 + (-4)2] = √(9 + 16) = √25 = 5.

Cas particulier: Distance à l'origine

Si l'un des points est l'origine O(0, 0), la formule se simplifie. La distance entre un point A(x, y) et l'origine est :

OA = √(x2 + y2).

Par exemple, la distance entre le point A(3, 4) et l'origine est √(32 + 42) = √25 = 5.

Importance du signe

Bien que l'on prenne souvent la valeur absolue de la différence des coordonnées pour simplifier, il est important de noter que le carré d'un nombre (positif ou négatif) est toujours positif. Le signe de (xB - xA) ou (yB - yA) n'affecte pas le résultat final du calcul de la distance.

Ce qu'il faut retenir

  • La distance entre deux points A(xA, yA) et B(xB, yB) est donnée par la formule : AB = √[(xB - xA)2 + (yB - yA)2].
  • Cette formule est une application du théorème de Pythagore.
  • La distance entre un point A(x, y) et l'origine est OA = √(x2 + y2).

← Applications et Exemples des Cercles, Ellipses et Hyperboles Calcul des Volumes : Prisme, Cylindre, Pyramide, Cône et Sphère →

FAQ

  • La distance peut-elle être négative ?

    Non, la distance est toujours une valeur positive ou nulle. Elle représente une longueur.
  • L'ordre des points A et B dans la formule affecte-t-il le résultat ?

    Non, la formule est symétrique. Inverser A et B ne change pas le résultat, car on élève au carré la différence des coordonnées.
  • Que faire si les points A et B ont la même abscisse ou la même ordonnée?

    Si A et B ont la même abscisse (xA = xB), la distance AB = |yB - yA|. Si A et B ont la même ordonnée (yA = yB), la distance AB = |xB - xA|.