Mathématiques > Analyse > Limites de Fonctions > Asymptotes (horizontales, verticales, obliques - notions)

Asymptotes : Horizontales, Verticales, Obliques

Comprendre et identifier les asymptotes horizontales, verticales et obliques d'une fonction. Définitions, exemples et méthodes pour le lycée.

Introduction aux Asymptotes

Les asymptotes sont des droites vers lesquelles la courbe représentative d'une fonction se rapproche infiniment sans jamais les toucher (ou parfois en les coupant en un point précis). Elles donnent des informations précieuses sur le comportement de la fonction aux 'bords' de son domaine de définition, c'est-à-dire lorsque x tend vers l'infini (positif ou négatif) ou vers une valeur particulière où la fonction n'est pas définie. Il existe trois types principaux d'asymptotes : horizontales, verticales et obliques. Dans ce cours, nous allons explorer chacune de ces asymptotes en détail, avec des exemples concrets pour faciliter la compréhension.

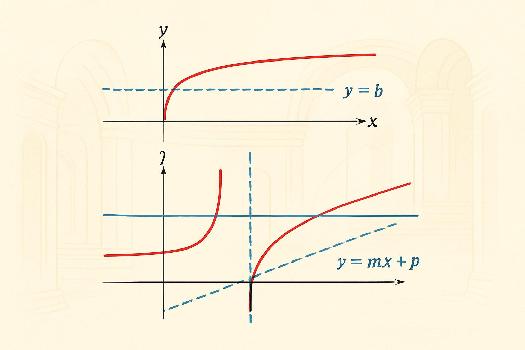
Asymptotes Horizontales

Une droite d'équation y = b est une asymptote horizontale à la courbe représentative de f si, lorsque x tend vers plus l'infini (+∞) ou moins l'infini (-∞), f(x) tend vers b. En d'autres termes,

Si limx→+∞ f(x) = b ou limx→-∞ f(x) = b, alors la droite y = b est une asymptote horizontale.

Exemple: Considérons la fonction f(x) = (2x + 1) / (x - 3).
Pour déterminer l'asymptote horizontale, on calcule les limites à l'infini:
limx→+∞ (2x + 1) / (x - 3) = 2 et limx→-∞ (2x + 1) / (x - 3) = 2.
Donc, la droite d'équation y = 2 est une asymptote horizontale.

Asymptotes Verticales

Une droite d'équation x = a est une asymptote verticale à la courbe représentative de f si, lorsque x tend vers a (par valeurs supérieures ou inférieures), f(x) tend vers plus l'infini (+∞) ou moins l'infini (-∞).

Autrement dit, si limx→a f(x) = +∞ ou limx→a f(x) = -∞, alors la droite x = a est une asymptote verticale. Il faut généralement regarder les limites à gauche (limx→a-) et à droite (limx→a+) de a.

Exemple: Considérons la fonction f(x) = 1 / (x - 2).
Cette fonction n'est pas définie en x = 2.
On calcule les limites: limx→2+ 1 / (x - 2) = +∞ et limx→2- 1 / (x - 2) = -∞.
Donc, la droite d'équation x = 2 est une asymptote verticale.

Asymptotes Obliques

Une droite d'équation y = mx + p (avec m ≠ 0) est une asymptote oblique à la courbe représentative de f si, lorsque x tend vers plus l'infini (+∞) ou moins l'infini (-∞), la différence entre f(x) et mx + p tend vers zéro.

En d'autres termes, si limx→+∞ [f(x) - (mx + p)] = 0 ou limx→-∞ [f(x) - (mx + p)] = 0, alors la droite y = mx + p est une asymptote oblique.

Méthode pour trouver une asymptote oblique:

  1. Calculer m : m = limx→+∞ f(x) / x (ou limx→-∞ f(x) / x). Si cette limite existe et est non nulle, on continue.
  2. Calculer p : p = limx→+∞ [f(x) - mx] (ou limx→-∞ [f(x) - mx]).

Exemple: Considérons la fonction f(x) = (x2 + 1) / x.
Calculons m : limx→+∞ (x2 + 1) / x2 = 1. Donc m = 1.
Calculons p : limx→+∞ [(x2 + 1) / x - x] = limx→+∞ 1 / x = 0. Donc p = 0.
L'asymptote oblique est donc la droite d'équation y = x.

Cas particulier : Fonction Rationnelle

Pour une fonction rationnelle f(x) = P(x) / Q(x), où P(x) et Q(x) sont des polynômes :

  • Asymptote Horizontale: Si le degré de P(x) est inférieur ou égal au degré de Q(x), alors il existe une asymptote horizontale.
  • Asymptote Verticale: Les asymptotes verticales se trouvent aux valeurs de x qui annulent le dénominateur Q(x), à condition que ces valeurs ne soient pas aussi des racines du numérateur P(x).
  • Asymptote Oblique: Si le degré de P(x) est exactement un de plus que le degré de Q(x), alors il existe une asymptote oblique. Elle peut être trouvée par division euclidienne de P(x) par Q(x). Le quotient sera de la forme mx + p, l'équation de l'asymptote.

Ce qu'il faut retenir

  • Asymptote Horizontale: limx→+∞ f(x) = b ou limx→-∞ f(x) = b, alors y = b est une asymptote horizontale.
  • Asymptote Verticale: limx→a f(x) = +∞ ou limx→a f(x) = -∞, alors x = a est une asymptote verticale.
  • Asymptote Oblique: Si limx→+∞ [f(x) - (mx + p)] = 0 ou limx→-∞ [f(x) - (mx + p)] = 0, alors y = mx + p est une asymptote oblique. Pour trouver m et p, calculez les limites successives décrites dans le cours.

← Applications des Équations et Inéquations Exponentielles et Logarithmiques Calcul Pratique des Limites: Exemples et Techniques →

FAQ

  • Comment savoir si une fonction a une asymptote horizontale ?

    Calculez les limites de la fonction lorsque x tend vers plus l'infini et moins l'infini. Si l'une de ces limites existe et est finie (égale à un nombre b), alors la droite d'équation y = b est une asymptote horizontale.
  • Comment trouver une asymptote verticale ?

    Recherchez les valeurs de x qui annulent le dénominateur de la fonction (si elle est sous forme de fraction) et vérifiez si la limite de la fonction lorsque x tend vers ces valeurs est infinie. Si c'est le cas, vous avez une asymptote verticale.
  • Quand est-ce qu'une fonction a une asymptote oblique et comment la trouver ?

    Une fonction a une asymptote oblique lorsque le degré du numérateur est exactement un de plus que le degré du dénominateur (pour une fonction rationnelle). Pour la trouver, divisez le numérateur par le dénominateur. Le quotient sera de la forme mx + p, qui est l'équation de l'asymptote oblique.