Mathématiques > Algèbre > Fonctions > Fonctions linéaires

Fonctions Linéaires et Proportionnalité

Explorez le lien entre les fonctions linéaires et la proportionnalité, avec des exemples pratiques et des exercices corrigés pour maîtriser ces concepts.

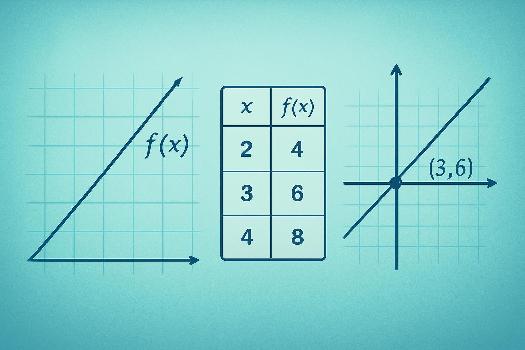
Rappel: Proportionnalité

Deux grandeurs sont proportionnelles si leur rapport est constant. Cela signifie que si une grandeur est multipliée par un facteur, l'autre est également multipliée par le même facteur. On peut représenter cette relation par un tableau de proportionnalité.

Fonction Linéaire et Proportionnalité : Le Lien

Une fonction linéaire f(x) = ax représente une situation de proportionnalité. x et f(x) sont proportionnels, et le coefficient directeur a est le coefficient de proportionnalité. Par exemple, si le prix d'un kilo de pommes est de 2 euros, la fonction f(x) = 2x représente le prix de x kilos de pommes. Le prix et le poids sont proportionnels, et le coefficient de proportionnalité est 2.

Tableau de Proportionnalité et Fonction Linéaire

On peut représenter une fonction linéaire par un tableau de proportionnalité. Par exemple, si f(x) = 3x, on a le tableau suivant:

x f(x)
0 0
1 3
2 6
On voit bien que f(x) est toujours égal à x multiplié par 3.

Exemples d'Applications

Voici quelques exemples où les fonctions linéaires modélisent des situations de proportionnalité:

  • Conversion d'unités: Convertir des degrés Celsius en degrés Fahrenheit suit une relation affine (et non linéaire) mais on peut convertir des euros en dollars si le taux de change est fixe.
  • Calcul d'intérêts simples: Les intérêts simples sont proportionnels au capital initial et au taux d'intérêt.
  • Échelle d'une carte: La distance sur une carte est proportionnelle à la distance réelle.

Exercices Corrigés

Exercice 1: Le prix d'un ticket de cinéma est de 8 euros. Écrire la fonction linéaire qui représente le prix de x tickets. Calculer le prix de 5 tickets. Correction: La fonction est f(x) = 8x. Le prix de 5 tickets est f(5) = 8 * 5 = 40 euros. Exercice 2: Un robinet fuit à un débit de 0.5 litre par heure. Écrire la fonction linéaire qui représente la quantité d'eau perdue en x heures. Calculer la quantité d'eau perdue en 24 heures. Correction: La fonction est f(x) = 0.5x. La quantité d'eau perdue en 24 heures est f(24) = 0.5 * 24 = 12 litres.

Ce qu'il faut retenir

  • Une fonction linéaire f(x) = ax représente une situation de proportionnalité.
  • x et f(x) sont proportionnels, et a est le coefficient de proportionnalité.
  • On peut représenter une fonction linéaire par un tableau de proportionnalité.
  • Les fonctions linéaires sont utilisées pour modéliser des situations de proportionnalité dans divers domaines.

← Fonctions Affines : Guide Complet et Exemples Fonctions Paires et Impaires : Comprendre et Identifier →

FAQ

  • Toutes les situations de proportionnalité peuvent-elles être modélisées par une fonction linéaire?

    Oui, toute situation de proportionnalité peut être modélisée par une fonction linéaire de la forme f(x) = ax, où a est le coefficient de proportionnalité.
  • Comment identifier une situation de proportionnalité?

    Une situation est proportionnelle si le rapport entre les deux grandeurs est constant. Cela signifie que si une grandeur est multipliée par un facteur, l'autre est également multipliée par le même facteur.
  • Quel est l'intérêt de modéliser une situation de proportionnalité par une fonction linéaire?

    Modéliser une situation de proportionnalité par une fonction linéaire permet de facilement calculer les valeurs de la grandeur dépendante en fonction de la grandeur indépendante, et de visualiser la relation entre les deux grandeurs sur un graphique.