Comprendre les Suites Numériques : Explicites et Récurrentes

Introduction aux Suites Numériques

Les suites numériques sont des listes ordonnées de nombres. Chaque nombre dans la suite est appelé un terme. Les suites sont fondamentales en mathématiques et apparaissent dans de nombreux domaines, allant de la physique à l'économie. On distingue principalement deux types de définitions pour les suites : les définitions explicites et les définitions récurrentes. Comprendre ces deux types de définitions est essentiel pour manipuler et étudier les suites.

Suite Définie de Manière Explicite

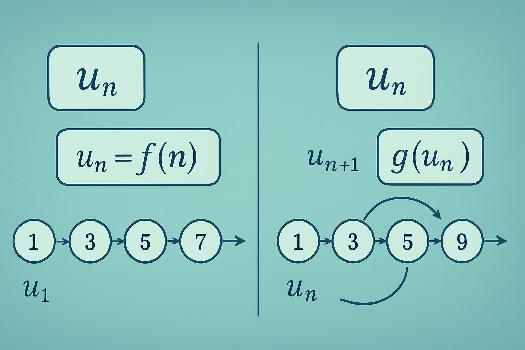
Une suite est dite définie de manière explicite si l'on peut calculer directement le terme général u_n en fonction de n, où n représente la position du terme dans la suite. En d'autres termes, on a une formule qui permet de trouver n'importe quel terme de la suite sans avoir besoin de connaître les termes précédents. Cette formule est généralement notée u_n = f(n), où f est une fonction.

Exemple: Considérons la suite définie par u_n = 2n + 1. Pour trouver le 5ème terme (u₅), il suffit de remplacer n par 5 dans la formule : u₅ = 2(5) + 1 = 11. De même, u₁₀ = 2(10) + 1 = 21. On peut ainsi calculer n'importe quel terme directement.

Avantage: La définition explicite permet de calculer n'importe quel terme rapidement, sans avoir besoin de calculer les termes précédents. Elle est particulièrement utile pour étudier le comportement de la suite lorsque n devient très grand.

Suite Définie de Manière Récurrente

Une suite est dite définie de manière récurrente si chaque terme est défini en fonction du ou des termes précédents. Cela signifie qu'on a besoin de connaître un ou plusieurs termes initiaux pour pouvoir calculer les termes suivants. Une définition récurrente se compose généralement d'une formule de récurrence qui relie u_n+1 à u_n (ou à plusieurs termes précédents) et d'une ou plusieurs valeurs initiales.

Exemple: Considérons la suite définie par u₀ = 1 et u_n+1 = 3u_n - 2. Pour trouver u₁, on utilise la formule de récurrence avec n = 0 : u₁ = 3u₀ - 2 = 3(1) - 2 = 1. Pour trouver u₂, on utilise la formule avec n = 1 : u₂ = 3u₁ - 2 = 3(1) - 2 = 1. Et ainsi de suite. On remarque qu'il est nécessaire de connaître le terme précédent pour calculer le terme suivant.

Avantage: La définition récurrente est souvent plus naturelle pour modéliser des phénomènes où l'état futur dépend de l'état présent. Par exemple, l'évolution d'une population peut être modélisée par une suite récurrente.

Inconvénient: Pour calculer un terme éloigné (par exemple, u₁₀₀), il faut calculer tous les termes précédents. Cependant, dans certains cas, il est possible de trouver une expression explicite à partir d'une définition récurrente (mais ce n'est pas toujours facile).

Exemples Comparatifs

Pour bien comprendre la différence entre les deux types de définitions, comparons deux suites qui convergent vers la même valeur:

Suite Explicite : u_n = 1 + (1/n) pour n ≥ 1. Ici, on peut directement calculer n'importe quel terme sans connaître les précédents. Par exemple, u₁₀ = 1 + (1/10) = 1.1.

Suite Récurrente : u₁ = 2 et u_n+1 = (u_n + 1)/2. Pour calculer u₂, on a besoin de u₁ : u₂ = (2 + 1)/2 = 1.5. De même, u₃ = (1.5 + 1)/2 = 1.25. On voit qu'on doit calculer chaque terme étape par étape.

Bien que ces deux suites convergent vers 1 lorsque n tend vers l'infini, leur façon d'être définies est fondamentalement différente. La suite explicite offre un calcul direct, tandis que la suite récurrente nécessite une progression séquentielle.

Passage d'une Définition Récurrente à une Définition Explicite

Il est parfois possible, mais pas toujours, de trouver une expression explicite pour une suite définie récursivement. Cette transformation peut être complexe et nécessite des techniques spécifiques. Voici quelques pistes générales :

1. Reconnaissance de motifs : Calculez les premiers termes de la suite et essayez de repérer un motif. Ce motif peut vous donner une idée de la forme de l'expression explicite.

2. Utilisation d'équations caractéristiques : Cette méthode est particulièrement utile pour les suites récurrentes linéaires, c'est-à-dire celles où chaque terme est une combinaison linéaire des termes précédents. Par exemple, pour une suite définie par u_n+2 = au_n+1 + bu_n, on peut résoudre l'équation caractéristique r² = ar + b. Les racines de cette équation permettent de trouver l'expression explicite de la suite.

3. Sommation télescopique : Cette technique consiste à transformer la relation de récurrence en une somme télescopique, c'est-à-dire une somme où la plupart des termes s'annulent.

Trouver l'expression explicite d'une suite récurrente est un problème souvent difficile et il n'existe pas de méthode universelle. Cependant, avec de la pratique et en utilisant les techniques appropriées, on peut résoudre de nombreux cas.

Ce qu'il faut retenir

• Une suite numérique est une liste ordonnée de nombres.
• Une suite peut être définie de manière explicite (u_n = f(n)) ou récurrente (u_n+1 = g(u_n)).
• Une définition explicite permet de calculer directement n'importe quel terme.
• Une définition récurrente nécessite de connaître les termes précédents pour calculer le terme suivant.
• Il est parfois possible de passer d'une définition récurrente à une définition explicite, mais ce n'est pas toujours facile.