Vecteurs : Définition, Opérations et Colinéarité

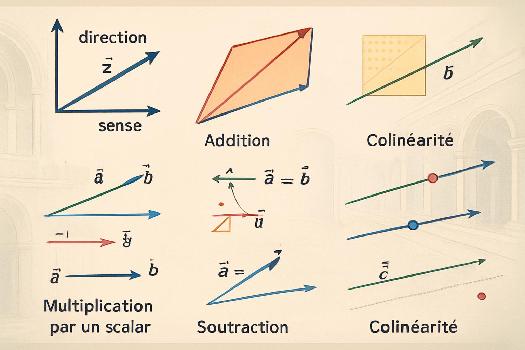
Définition d'un Vecteur

Un vecteur est une entité mathématique définie par trois caractéristiques principales : une direction, un sens et une norme (ou longueur). Géométriquement, un vecteur est représenté par un segment orienté, c'est-à-dire une flèche.

On note un vecteur avec une flèche au-dessus, par exemple $\overrightarrow{\mathrm{AB}}$ , où A est l'origine et B est l'extrémité du vecteur. La norme du vecteur $\overrightarrow{\mathrm{AB}}$ est notée ||$\overrightarrow{\mathrm{AB}}$|| et représente la distance entre A et B.

Deux vecteurs sont dits égaux s'ils ont la même direction, le même sens et la même norme.

Addition Vectorielle

L'addition de vecteurs peut se faire de deux manières principales :

1. Méthode du parallélogramme : Si l'on veut additionner deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ ayant la même origine, on construit un parallélogramme dont les côtés sont définis par les deux vecteurs. La diagonale du parallélogramme issue de l'origine commune représente le vecteur somme $\overrightarrow{u}$ + $\overrightarrow{v}$.
2. Relation de Chasles : Pour additionner les vecteurs $\overrightarrow{\mathrm{AB}}$ et $\overrightarrow{\mathrm{BC}}$, la relation de Chasles stipule que $\overrightarrow{\mathrm{AB}}$ + $\overrightarrow{\mathrm{BC}}$ = $\overrightarrow{\mathrm{AC}}$. C'est-à-dire que l'extrémité du premier vecteur coïncide avec l'origine du second.

Soustraction Vectorielle

La soustraction de vecteurs $\overrightarrow{u}$ - $\overrightarrow{v}$ est définie comme l'addition du vecteur $\overrightarrow{u}$ avec l'opposé du vecteur $\overrightarrow{v}$ (noté -$\overrightarrow{v}$). Le vecteur -$\overrightarrow{v}$ a la même direction et la même norme que $\overrightarrow{v}$, mais son sens est opposé.

Donc, $\overrightarrow{u}$ - $\overrightarrow{v}$ = $\overrightarrow{u}$ + (-$\overrightarrow{v}$). Géométriquement, cela revient à inverser le sens du vecteur $\overrightarrow{v}$ et à l'ajouter au vecteur $\overrightarrow{u}$ selon la méthode du parallélogramme ou la relation de Chasles.

Multiplication d'un Vecteur par un Scalaire

La multiplication d'un vecteur par un scalaire (un nombre réel) change la norme du vecteur. Si k est un scalaire et $\overrightarrow{u}$ un vecteur, alors k$\overrightarrow{u}$ est un vecteur qui a :

• La même direction que $\overrightarrow{u}$.
• Un sens qui est le même que celui de $\overrightarrow{u}$ si k > 0, et opposé si k < 0.
• Une norme qui est |k| fois la norme de $\overrightarrow{u}$, c'est-à-dire ||k$\overrightarrow{u}$|| = |k| ||$\overrightarrow{u}$||.

Colinéarité de Vecteurs

Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont dits colinéaires s'ils ont la même direction. Cela signifie qu'il existe un scalaire k tel que $\overrightarrow{u}$ = k$\overrightarrow{v}$ ou $\overrightarrow{v}$ = k$\overrightarrow{u}$. Si deux vecteurs sont colinéaires, alors les droites qu'ils définissent sont parallèles.

Conséquences :

• Si $\overrightarrow{\mathrm{AB}}$ et $\overrightarrow{\mathrm{AC}}$ sont colinéaires, alors les points A, B et C sont alignés.
• Dans un repère, si $\overrightarrow{u}$(x ; y) et $\overrightarrow{v}$(x' ; y') sont colinéaires, alors leur déterminant est nul : xy' - x'y = 0.

Ce qu'il faut retenir

• Définition d'un vecteur : Direction, sens, norme.
• Addition vectorielle : Méthode du parallélogramme, relation de Chasles.
• Soustraction vectorielle : Addition de l'opposé du vecteur.
• Multiplication par un scalaire : Change la norme du vecteur.
• Colinéarité : Vecteurs de même direction, déterminant nul (dans un repère). Alignement de points.