Mathématiques > Algèbre > Polynômes > Définition et vocabulaire (degré, coefficients)

Polynômes : Définition, Degré et Coefficients

Ce cours complet sur les polynômes est conçu pour les élèves de lycée. Il couvre la définition formelle, le vocabulaire essentiel (degré, coefficients), et illustre les concepts avec des exemples concrets. Maîtrisez les bases de l'algèbre polynomiale !

Définition d'un Polynôme

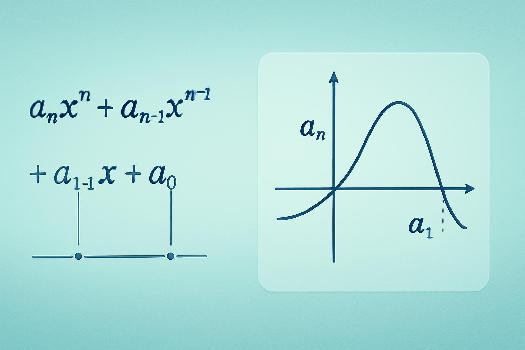
Un polynôme est une expression mathématique composée de variables (souvent désignées par 'x') et de coefficients, combinés à l'aide d'opérations d'addition, de soustraction et de multiplication, avec des exposants entiers non négatifs. Plus formellement, un polynôme P(x) peut s'écrire sous la forme suivante: P(x) = anxn + an-1xn-1 + ... + a1x + a0 Où:

  • x est la variable.
  • an, an-1, ..., a1, a0 sont les coefficients (des nombres réels ou complexes).
  • n est un entier non négatif représentant le degré du terme correspondant.
Exemple : 3x2 + 2x - 5 est un polynôme.

Vocabulaire Essentiel

Comprendre le vocabulaire associé aux polynômes est crucial. Voici les termes clés:

  • Terme : Chaque élément de la somme dans le polynôme (par exemple, 3x2, 2x, -5).
  • Coefficient : Le nombre qui multiplie la variable dans un terme (par exemple, 3 dans 3x2, 2 dans 2x, -5 dans -5).
  • Degré d'un terme : L'exposant de la variable dans un terme (par exemple, 2 dans 3x2, 1 dans 2x, 0 dans -5 car -5 = -5x0).
  • Terme constant : Le terme qui ne contient pas de variable (par exemple, -5). Il est aussi appelé terme de degré 0.
  • Polynôme nul : Un polynôme dont tous les coefficients sont égaux à zéro. Il n'a pas de degré défini.

Degré d'un Polynôme

Le degré d'un polynôme est le plus grand degré de ses termes non nuls. En d'autres termes, c'est la plus haute puissance de la variable 'x' qui apparaît dans le polynôme. Exemple : Dans le polynôme P(x) = 5x4 - 2x2 + x - 7, le terme de plus haut degré est 5x4, donc le degré du polynôme est 4. On dit que P(x) est un polynôme de degré 4. Si tous les coefficients d'un polynôme sont nuls, le polynôme est dit nul et son degré n'est pas défini. Voici quelques exemples: * P(x) = 7x + 3 est un polynôme de degré 1 (polynôme linéaire). * P(x) = 2x2 - 5x + 1 est un polynôme de degré 2 (polynôme quadratique). * P(x) = x3 + 4x2 - 6x + 8 est un polynôme de degré 3 (polynôme cubique). * P(x) = 9 est un polynôme de degré 0 (polynôme constant).

Coefficients d'un Polynôme

Les coefficients d'un polynôme sont les nombres qui multiplient les variables 'x' élevées à différentes puissances. Ils peuvent être des nombres réels ou complexes. Dans le polynôme P(x) = anxn + an-1xn-1 + ... + a1x + a0:

  • an est le coefficient du terme de degré n.
  • an-1 est le coefficient du terme de degré n-1.
  • ...
  • a1 est le coefficient du terme de degré 1.
  • a0 est le coefficient du terme de degré 0 (le terme constant).
Exemple : Dans le polynôme P(x) = 7x3 - 4x2 + 2x + 9:
  • Le coefficient de x3 est 7.
  • Le coefficient de x2 est -4.
  • Le coefficient de x est 2.
  • Le terme constant est 9.

Exemples et Exercices

Essayons quelques exemples pour bien comprendre: Exemple 1 : P(x) = -2x5 + 3x3 - x + 6 * Degré du polynôme: 5 * Coefficient du terme de degré 5: -2 * Coefficient du terme de degré 3: 3 * Coefficient du terme de degré 1: -1 * Terme constant: 6 Exemple 2 : Q(x) = 4x2 - 9 * Degré du polynôme: 2 * Coefficient du terme de degré 2: 4 * Coefficient du terme de degré 0: -9 Exercice : Déterminez le degré et les coefficients du polynôme suivant: R(x) = x4 + 5x2 - 2x + 1

Ce qu'il faut retenir

  • Définition d'un polynôme : Expression de la forme anxn + an-1xn-1 + ... + a1x + a0.
  • Degré d'un polynôme : Le plus grand exposant de la variable 'x'.
  • Coefficients : Les nombres qui multiplient les variables 'x' (par exemple, an, an-1, ..., a0).
  • Terme constant : Le terme sans variable (degré 0).
  • Bien identifier le degré et les coefficients d'un polynôme est essentiel pour manipuler et résoudre des équations polynomiales.

← Opérations sur les Polynômes : Addition, Soustraction, Multiplication Racines d'un polynôme : Définitions, méthodes et exemples →

FAQ

  • Le degré d'un polynôme peut-il être négatif ?

    Non, le degré d'un polynôme est toujours un entier non négatif.
  • Quel est le degré du polynôme nul ?

    Le degré du polynôme nul n'est pas défini.
  • Le coefficient dominant est-il toujours le premier coefficient que l'on rencontre en lisant un polynôme de gauche à droite ?

    Non, le coefficient dominant est le coefficient du terme de plus haut degré. Il faut bien identifier le degré du polynôme avant d'identifier le coefficient dominant. Par exemple, dans le polynôme 3x + 5x2 -1, le coefficient dominant est 5.