Mathématiques > Géométrie > Géométrie Plane > Vecteurs (définition, opérations, colinéarité)

Applications des Vecteurs en Géométrie Plane

Ce document explore les applications pratiques des vecteurs en géométrie plane, notamment pour démontrer l'alignement de points et le parallélisme de droites. Destiné aux élèves de lycée.

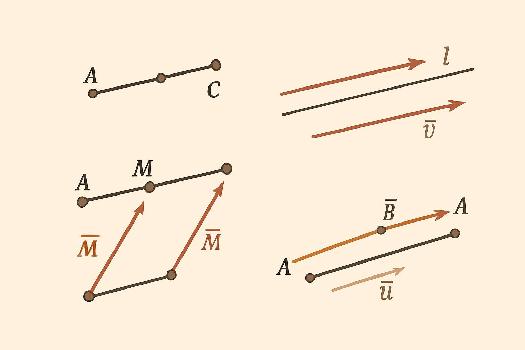
Alignement de Points

Pour démontrer que trois points A, B et C sont alignés, on peut montrer que les vecteurs AB→ et AC→ (ou BA→ et BC→, etc.) sont colinéaires. Autrement dit, on cherche à montrer qu'il existe un scalaire k tel que AB→ = kAC→. Si l'on parvient à trouver un tel k, alors les points A, B et C sont alignés.

Exemple : Soient A(1; 2), B(3; 6) et C(5; 10). On a AB→(2; 4) et AC→(4; 8). On observe que AC→ = 2AB→. Donc les vecteurs sont colinéaires, et les points A, B et C sont alignés.

Parallélisme de Droites

Pour démontrer que deux droites (AB) et (CD) sont parallèles, on peut montrer que les vecteurs directeurs AB→ et CD→ sont colinéaires. Encore une fois, on cherche à montrer qu'il existe un scalaire k tel que AB→ = kCD→.

Exemple : Soient A(0; 0), B(1; 2), C(2; 1) et D(3; 3). On a AB→(1; 2) et CD→(1; 2). On observe que AB→ = CD→ (donc k=1). Donc les vecteurs sont colinéaires, et les droites (AB) et (CD) sont parallèles.

Démonstration de Milieux

Pour démontrer qu'un point I est le milieu d'un segment [AB], on peut montrer que AI→ = IB→ ou que AI→ = 1/2 AB→.

Exemple : Soient A(1; 1), B(5; 3) et I(3; 2). On a AI→(2; 1) et IB→(2; 1). Donc AI→ = IB→, et I est le milieu de [AB].

Utilisation des vecteurs pour les Translations

Une translation de vecteur u→ transforme un point A en un point A' tel que AA'→ = u→. On peut utiliser cette propriété pour déterminer les coordonnées de l'image d'un point par une translation.

Exemple: Si on translate le point A(1;1) par le vecteur u→(2;3), alors l'image A' a pour coordonnées (1+2; 1+3) soit A'(3;4).

Ce qu'il faut retenir

  • Alignement de points : Démontrer la colinéarité des vecteurs formés par ces points.
  • Parallélisme de droites : Démontrer la colinéarité des vecteurs directeurs des droites.
  • Milieu d'un segment : Montrer que les vecteurs formés par le milieu et les extrémités sont égaux.
  • Translations : Utiliser la relation AA'→ = u→ pour trouver l'image d'un point.

← Angles et Trigonométrie dans le Triangle Rectangle : Guide Complet Applications et Exemples des Cercles, Ellipses et Hyperboles →

FAQ

  • Peut-on utiliser les vecteurs pour prouver qu'un quadrilatère est un parallélogramme ?

    Oui, un quadrilatère ABCD est un parallélogramme si AB→ = DC→ ou AD→ = BC→.
  • Comment utiliser les vecteurs pour démontrer qu'un triangle est rectangle ?

    On ne démontre pas directement qu'un triangle est rectangle avec les vecteurs de cette manière. On utilise plutôt le produit scalaire (qui n'est pas couvert ici). Cependant, si vous connaissez les longueurs des côtés, vous pouvez utiliser le théorème de Pythagore.