Mathématiques > Géométrie > Géométrie Spatiale > Repérage dans l'espace (coordonnées cartésiennes)

Repérage dans l'espace : Coordonnées Cartésiennes

Comprendre le repérage dans l'espace grâce aux coordonnées cartésiennes : un guide complet pour les lycéens avec définitions, exemples et exercices.

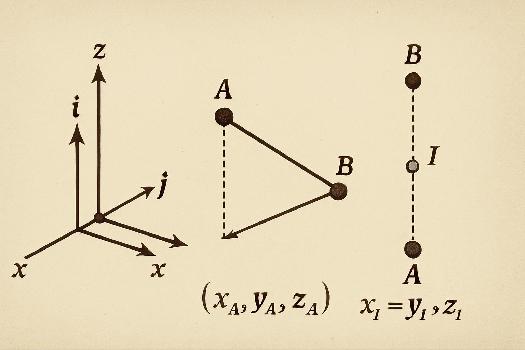
Introduction au repérage dans l'espace

Dans le plan, nous utilisons deux axes (x et y) pour repérer un point. Dans l'espace, nous ajoutons un troisième axe (z) perpendiculaire aux deux autres. Ce système de trois axes forme ce qu'on appelle un repère cartésien. Imaginez le coin d'une pièce : les deux murs représentent les axes x et y, et la hauteur représente l'axe z. Chaque point dans l'espace est alors défini par trois coordonnées : (x, y, z).

Le repère cartésien (O, i, j, k)

Un repère cartésien est composé d'un point d'origine O (l'intersection des trois axes) et de trois vecteurs unitaires orthogonaux : i, j, et k.

i est un vecteur de longueur 1 dirigé le long de l'axe x.

j est un vecteur de longueur 1 dirigé le long de l'axe y.

k est un vecteur de longueur 1 dirigé le long de l'axe z.

Ce repère est noté (O, i, j, k).

Définition des coordonnées d'un point

Soit un point M dans l'espace. Ses coordonnées (x, y, z) dans le repère (O, i, j, k) sont définies de la manière suivante:

Le vecteur OM peut être décomposé en une combinaison linéaire des vecteurs i, j, et k :

OM = xi + yj + zk.

x est l'abscisse du point M (sa position sur l'axe x).

y est l'ordonnée du point M (sa position sur l'axe y).

z est la cote du point M (sa position sur l'axe z).

Autrement dit, pour atteindre le point M depuis l'origine O, il faut se déplacer de x unités dans la direction de i, puis de y unités dans la direction de j, et enfin de z unités dans la direction de k.

Exemples concrets

Exemple 1: Le point A (2, 3, 1) signifie qu'à partir de l'origine O, il faut avancer de 2 unités selon l'axe x, de 3 unités selon l'axe y, et de 1 unité selon l'axe z.

Exemple 2: Le point B (-1, 0, 4) signifie qu'à partir de l'origine O, il faut reculer de 1 unité selon l'axe x, ne pas se déplacer selon l'axe y, et monter de 4 unités selon l'axe z.

Exemple 3: Le point C (0, -2, 0) signifie qu'à partir de l'origine O, il ne faut pas se déplacer selon l'axe x, reculer de 2 unités selon l'axe y, et ne pas se déplacer selon l'axe z. Ce point se situe sur l'axe des ordonnées.

Calcul de la distance entre deux points

Soient deux points A(xA, yA, zA) et B(xB, yB, zB) dans l'espace. La distance entre A et B, notée AB, est donnée par la formule suivante :

AB = √((xB - xA)2 + (yB - yA)2 + (zB - zA)2)

Cette formule est une extension du théorème de Pythagore en trois dimensions.

Exemple de calcul de distance

Soient les points A(1, 2, 3) et B(4, -2, 1). Calculons la distance AB.

AB = √((4 - 1)2 + (-2 - 2)2 + (1 - 3)2)

AB = √((3)2 + (-4)2 + (-2)2)

AB = √(9 + 16 + 4)

AB = √29

Donc, la distance entre A et B est √29 unités.

Coordonnées du milieu d'un segment

Soient deux points A(xA, yA, zA) et B(xB, yB, zB) dans l'espace. Les coordonnées du milieu I du segment [AB] sont données par :

xI = (xA + xB) / 2

yI = (yA + yB) / 2

zI = (zA + zB) / 2

Exemple de calcul des coordonnées du milieu

Soient les points A(1, 2, 3) et B(5, 0, 1). Calculons les coordonnées du milieu I du segment [AB].

xI = (1 + 5) / 2 = 3

yI = (2 + 0) / 2 = 1

zI = (3 + 1) / 2 = 2

Donc, les coordonnées du milieu I sont (3, 1, 2).

Applications

Le repérage dans l'espace est essentiel dans de nombreux domaines :

  • Infographie et jeux vidéo : Pour la modélisation 3D et le rendu d'objets et de scènes.
  • Navigation : Systèmes GPS utilisent des coordonnées spatiales pour déterminer la position.
  • Architecture et ingénierie : Pour la conception et la construction de bâtiments et d'infrastructures.
  • Physique : Pour décrire le mouvement des objets dans l'espace.

Ce qu'il faut retenir

  • Un point dans l'espace est repéré par trois coordonnées : (x, y, z).
  • Le repère cartésien est défini par un point d'origine O et trois vecteurs unitaires orthogonaux i, j, k.
  • La distance entre deux points A(xA, yA, zA) et B(xB, yB, zB) est donnée par AB = √((xB - xA)2 + (yB - yA)2 + (zB - zA)2).
  • Les coordonnées du milieu I du segment [AB] sont : xI = (xA + xB) / 2, yI = (yA + yB) / 2, zI = (zA + zB) / 2.

← Représentation graphique des fonctions sinus et cosinus Résolution de problèmes géométriques avec les coordonnées →

FAQ

  • Comment déterminer les coordonnées d'un point dans l'espace à partir d'un dessin ?

    Il faut projeter le point sur chacun des axes x, y et z. La valeur de la projection sur chaque axe correspond à la coordonnée correspondante.
  • Le repère cartésien est-il le seul système de coordonnées possible dans l'espace ?

    Non, il existe d'autres systèmes de coordonnées, comme les coordonnées cylindriques ou sphériques, qui sont plus adaptés à certaines situations.
  • Pourquoi les axes doivent-ils être orthogonaux dans un repère cartésien ?

    L'orthogonalité des axes simplifie les calculs et permet une représentation claire et intuitive de l'espace.