Mathématiques > Géométrie > Trigonométrie > Valeurs remarquables des fonctions trigonométriques

Maîtriser les valeurs remarquables des fonctions trigonométriques

Ce guide complet détaille les valeurs remarquables des fonctions sinus, cosinus et tangente pour les angles courants (0, π/6, π/4, π/3, π/2), avec des explications claires, des exemples et des astuces pour les mémoriser.

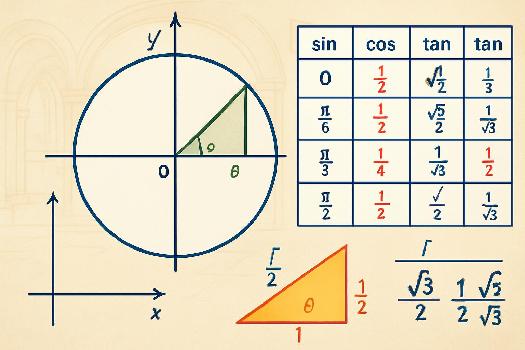
Introduction aux valeurs remarquables

Comprendre les valeurs remarquables des fonctions trigonométriques (sinus, cosinus, tangente) pour certains angles spécifiques est crucial en trigonométrie. Ces valeurs apparaissent fréquemment dans les problèmes et les applications, et les connaître permet de résoudre rapidement de nombreux exercices. Les angles concernés sont généralement 0, π/6 (30°), π/4 (45°), π/3 (60°) et π/2 (90°).

Le cercle trigonométrique : un outil indispensable

Le cercle trigonométrique est un cercle de rayon 1 centré à l'origine d'un repère orthonormé. Un angle θ, mesuré en radians, est représenté par un point sur le cercle. L'abscisse de ce point est égale à cos(θ) et l'ordonnée est égale à sin(θ). Utiliser le cercle trigonométrique permet de visualiser facilement les valeurs du sinus et du cosinus pour différents angles.

Rappel essentiel : Sur le cercle trigonométrique, le cosinus se lit sur l'axe des abscisses (l'axe horizontal), et le sinus se lit sur l'axe des ordonnées (l'axe vertical).

Valeurs remarquables du sinus

Voici les valeurs remarquables du sinus, qu'il est important de connaître :

  • sin(0) = 0
  • sin(π/6) = 1/2
  • sin(π/4) = √2/2
  • sin(π/3) = √3/2
  • sin(π/2) = 1

Astuce : On peut remarquer que les valeurs du sinus augmentent de 0 à 1 en passant par des fractions avec √ dans l'ordre 0, 1, 2, 3, 4 au numérateur, divisées par 2. Autrement dit, on a sin(x) = √(n)/2, où n prend les valeurs 0, 1, 2, 3, 4 pour x = 0, π/6, π/4, π/3, π/2 respectivement.

Valeurs remarquables du cosinus

Voici les valeurs remarquables du cosinus :

  • cos(0) = 1
  • cos(π/6) = √3/2
  • cos(π/4) = √2/2
  • cos(π/3) = 1/2
  • cos(π/2) = 0

Astuce : On remarque que les valeurs du cosinus sont les mêmes que celles du sinus, mais dans l'ordre inverse. Ainsi, cos(θ) = sin(π/2 - θ).

Valeurs remarquables de la tangente

La tangente est définie comme le rapport du sinus sur le cosinus : tan(θ) = sin(θ) / cos(θ). On peut donc calculer les valeurs remarquables de la tangente à partir des valeurs du sinus et du cosinus :

  • tan(0) = sin(0) / cos(0) = 0 / 1 = 0
  • tan(π/6) = sin(π/6) / cos(π/6) = (1/2) / (√3/2) = 1/√3 = √3/3
  • tan(π/4) = sin(π/4) / cos(π/4) = (√2/2) / (√2/2) = 1
  • tan(π/3) = sin(π/3) / cos(π/3) = (√3/2) / (1/2) = √3
  • tan(π/2) = sin(π/2) / cos(π/2) = 1 / 0 = Indéfinie (la tangente n'est pas définie en π/2)

Résumé :
  • tan(0) = 0
  • tan(π/6) = √3/3
  • tan(π/4) = 1
  • tan(π/3) = √3
  • tan(π/2) = Indéfinie

Mémorisation : tableau récapitulatif

Un tableau récapitulatif peut grandement faciliter la mémorisation :

Angle (radians)Angle (degrés)sin(θ)cos(θ)tan(θ)
00°010
π/630°1/2√3/2√3/3
π/445°√2/2√2/21
π/360°√3/21/2√3
π/290°10Indéfinie

Exemples d'application

Exemple 1 : Calculer sin(5π/6).
Solution : 5π/6 = π - π/6. On sait que sin(π - θ) = sin(θ), donc sin(5π/6) = sin(π/6) = 1/2.

Exemple 2 : Résoudre l'équation cos(x) = √3/2, où x ∈ [0, 2π].
Solution : On sait que cos(π/6) = √3/2. De plus, cos(-θ) = cos(θ), donc cos(-π/6) = cos(π/6) = √3/2. Or, -π/6 n'est pas dans l'intervalle [0, 2π]. Cependant, cos(2π - θ) = cos(θ), donc cos(2π - π/6) = cos(11π/6) = √3/2. Les solutions sont donc x = π/6 et x = 11π/6.

Ce qu'il faut retenir

  • Les valeurs remarquables des fonctions trigonométriques sont essentielles pour résoudre rapidement des problèmes.
  • Le cercle trigonométrique est un outil visuel puissant pour comprendre ces valeurs.
  • Connaître les valeurs de sin(θ) et cos(θ) pour 0, π/6, π/4, π/3 et π/2 permet de déduire celles de tan(θ).
  • Il existe des astuces mnémotechniques pour retenir ces valeurs plus facilement.

← Maîtriser le Produit Scalaire : Exercices et Applications Complexes Orthogonalité de Deux Droites dans l'Espace →

FAQ

  • Comment puis-je me souvenir facilement des valeurs remarquables du sinus et du cosinus ?

    Visualisez le cercle trigonométrique. Rappelez-vous que le sinus est l'ordonnée et le cosinus est l'abscisse. Utilisez le tableau récapitulatif et entraînez-vous à le compléter de mémoire. La pratique régulière est la clé !
  • Pourquoi la tangente n'est-elle pas définie en π/2 ?

    Parce que cos(π/2) = 0, et la division par zéro est indéfinie. La tangente est définie comme sin(θ)/cos(θ), donc lorsque cos(θ) = 0, la tangente n'existe pas.
  • Où puis-je trouver d'autres exemples d'applications des valeurs remarquables ?

    Consultez votre manuel scolaire, recherchez des exercices en ligne ou demandez à votre professeur de vous fournir des exemples supplémentaires. La résolution de nombreux problèmes vous aidera à maîtriser ces concepts.