Mathématiques > Algèbre > Équations et Inéquations > Équations avec valeurs absolues

Équations avec Valeurs Absolues : Méthodes et Exemples

Apprenez à résoudre des équations impliquant des valeurs absolues grâce à ce guide détaillé. Nous aborderons les définitions, les propriétés et les méthodes de résolution avec de nombreux exemples concrets.

Définition et Propriétés de la Valeur Absolue

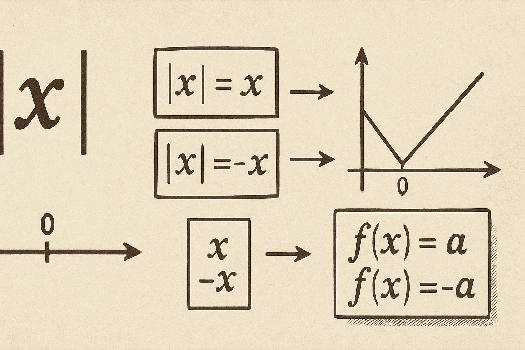
La valeur absolue d'un nombre réel x, notée |x|, est sa distance à zéro sur la droite numérique. Plus formellement:

  • Si x ≥ 0, alors |x| = x.
  • Si x < 0, alors |x| = -x.
Comprendre cette définition est crucial car elle implique que la valeur absolue d'un nombre est toujours non négative.

Quelques propriétés importantes:
  • |x| ≥ 0 pour tout x ∈ ℝ.
  • |-x| = |x| pour tout x ∈ ℝ.
  • |x * y| = |x| * |y| pour tous x, y ∈ ℝ.
  • |x / y| = |x| / |y| pour tous x, y ∈ ℝ (avec y ≠ 0).
Ces propriétés sont essentielles pour manipuler et simplifier des expressions contenant des valeurs absolues.

Méthodes de Résolution des Équations avec Valeurs Absolues

La résolution d'équations avec valeurs absolues repose sur le principe de considérer les deux cas possibles en raison de la définition de la valeur absolue. Voici les étapes générales :

1. Isoler la valeur absolue: Si possible, isolez l'expression contenant la valeur absolue d'un côté de l'équation.

2. Considérer les deux cas: Soit l'expression à l'intérieur de la valeur absolue est positive ou nulle, soit elle est négative. Établissez deux équations en conséquence:
* Cas 1: L'expression à l'intérieur de la valeur absolue est égale à la valeur de l'autre côté de l'équation.
* Cas 2: L'expression à l'intérieur de la valeur absolue est égale à l'opposé de la valeur de l'autre côté de l'équation.

3. Résoudre chaque équation: Résolvez chaque équation obtenue séparément.

4. Vérifier les solutions: Il est impératif de vérifier si les solutions obtenues dans chaque cas satisfont l'équation originale. Certaines solutions peuvent être extrêmes (non valides) à cause de la valeur absolue. Remplacez chaque solution dans l'équation d'origine et vérifiez si l'égalité est vraie.

Nous allons maintenant illustrer cette méthode avec des exemples.

Exemple 1 : |x - 3| = 5

Ici, la valeur absolue est déjà isolée. Nous devons considérer les deux cas:

Cas 1: x - 3 = 5
En ajoutant 3 aux deux côtés, nous obtenons x = 8.

Cas 2: x - 3 = -5
En ajoutant 3 aux deux côtés, nous obtenons x = -2.

Vérification:

  • Pour x = 8: |8 - 3| = |5| = 5 (OK)
  • Pour x = -2: |-2 - 3| = |-5| = 5 (OK)
Les deux solutions sont valides. L'ensemble des solutions est donc S = {-2, 8}.

Exemple 2 : |2x + 1| = 3x - 4

Cas 1: 2x + 1 = 3x - 4
En soustrayant 2x des deux côtés, on obtient 1 = x - 4. En ajoutant 4 aux deux côtés, on obtient x = 5.

Cas 2: 2x + 1 = -(3x - 4) ⇒ 2x + 1 = -3x + 4
En ajoutant 3x aux deux côtés, on obtient 5x + 1 = 4. En soustrayant 1 des deux côtés, on obtient 5x = 3. En divisant par 5, on obtient x = 3/5.

Vérification:

  • Pour x = 5: |2(5) + 1| = |11| = 11 et 3(5) - 4 = 15 - 4 = 11 (OK)
  • Pour x = 3/5: |2(3/5) + 1| = |6/5 + 5/5| = |11/5| = 11/5 et 3(3/5) - 4 = 9/5 - 20/5 = -11/5 (NON !)
x = 3/5 est une solution extrêmes (non valide). La seule solution valide est x = 5. L'ensemble des solutions est donc S = {5}.

Équations avec Valeurs Absolues Imbriquées

Parfois, vous rencontrerez des équations avec des valeurs absolues à l'intérieur d'autres valeurs absolues. La méthode reste la même, mais il faut l'appliquer étape par étape, en partant de la valeur absolue la plus interne vers l'extérieure.

Exemple : ||x - 1| - 2| = 1

Cas 1 : |x - 1| - 2 = 1
En ajoutant 2 des deux cotés, on obtient |x - 1| = 3. On se ramène à une équation avec une seul valeur absolue.
* Sous-cas 1: x - 1 = 3 ⇒ x = 4
* Sous-cas 2: x - 1 = -3 ⇒ x = -2

Cas 2 : |x - 1| - 2 = -1
En ajoutant 2 des deux cotés, on obtient |x - 1| = 1.
* Sous-cas 1: x - 1 = 1 ⇒ x = 2
* Sous-cas 2: x - 1 = -1 ⇒ x = 0

Vérification (laissée au lecteur) : Les quatres solutions sont valides. L'ensemble des solutions est donc S = {-2, 0, 2, 4}.

Ce qu'il faut retenir

  • La valeur absolue d'un nombre est sa distance à zéro.
  • |x| = x si x ≥ 0 et |x| = -x si x < 0.
  • Pour résoudre |f(x)| = a (où a ≥ 0), on résout f(x) = a et f(x) = -a.
  • Vérifiez toujours vos solutions dans l'équation originale!

← Utilisation du Tableau de Signe pour les Inéquations du Second Degré Équations du second degré : Méthodes de résolution et applications →

FAQ

  • Pourquoi dois-je vérifier les solutions d'une équation avec valeur absolue ?

    Parce que la valeur absolue peut introduire des solutions 'extrêmes'. En considérant les deux cas (positif et négatif), on peut trouver des valeurs de x qui satisfont les équations intermédiaires, mais pas l'équation d'origine à cause de la nature non-négative de la valeur absolue.
  • Que faire si j'ai une équation de la forme |f(x)| = g(x) ?

    Vous devez résoudre f(x) = g(x) et f(x) = -g(x), mais il est crucial de vérifier que les solutions obtenues satisfont la condition g(x) ≥ 0. Si g(x) est négatif pour une solution donnée, cette solution est extrêmes.