Introduction aux Graphes : Définitions et Vocabulaire

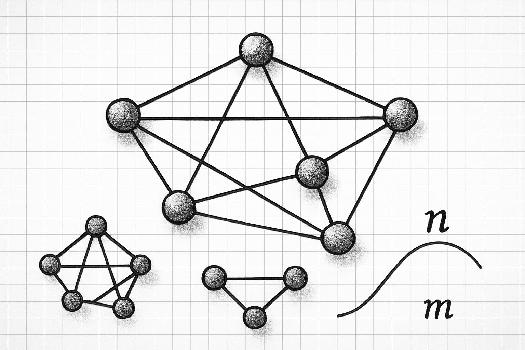
Qu'est-ce qu'un graphe ?

Un graphe est une structure mathématique qui représente des relations entre des objets. Imaginez un réseau social où les personnes sont connectées les unes aux autres. Un graphe est une façon d'illustrer ce réseau de manière formelle. Plus précisément, un graphe est composé de deux ensembles :

• Sommets (ou nœuds) : Ce sont les objets que l'on relie entre eux. Dans l'exemple du réseau social, ce seraient les personnes.
• Arêtes (ou liens) : Ce sont les connexions entre les sommets. Dans le réseau social, ce seraient les liens d'amitié.

Définition formelle

Mathématiquement, un graphe G est défini comme une paire ordonnée G = (V, E) où :

• V est un ensemble de sommets.
• E est un ensemble d'arêtes. Chaque arête est une paire de sommets. Si l'arête est non orientée, l'ordre de la paire n'a pas d'importance (par exemple, {A, B} est la même arête que {B, A}). Si l'arête est orientée, l'ordre compte (par exemple, (A, B) est différent de (B, A)).

Sommets et Arêtes : Les éléments de base

Sommets : Chaque point du graphe est un sommet. On les représente souvent par des points ou des cercles. Ils sont généralement identifiés par des lettres (A, B, C...) ou des nombres (1, 2, 3...).

Arêtes : Une arête relie deux sommets. On la représente par un trait (une ligne). Dans un graphe non orienté, une arête entre A et B indique une relation bidirectionnelle (A est lié à B, et B est lié à A). Dans un graphe orienté, l'arête a une direction (A est lié à B, mais pas nécessairement l'inverse). On représente une arête orientée par une flèche. Si une arête relie un sommet à lui-même, on l'appelle une boucle.

Ordre et Taille : Mesurer un graphe

Ordre d'un graphe : C'est le nombre de sommets dans le graphe. On le note souvent |V|.

Taille d'un graphe : C'est le nombre d'arêtes dans le graphe. On le note souvent |E|.

Exemple : Un graphe avec 5 sommets et 7 arêtes a un ordre de 5 et une taille de 7.

Exemple concret

Considérons un graphe représentant un réseau routier entre plusieurs villes :

• Les sommets sont les villes : A, B, C, D.
• Les arêtes sont les routes entre les villes : (A, B), (B, C), (C, D), (A, D), (B, D).

• L'ordre du graphe est 4 (il y a 4 villes).
• La taille du graphe est 5 (il y a 5 routes).

Vocabulaire additionnel

Il existe d'autres termes importants à connaître :

• Graphe simple : Un graphe sans boucle et sans arêtes multiples (plus d'une arête entre deux mêmes sommets).
• Graphe complet : Un graphe où chaque sommet est connecté à tous les autres sommets.
• Graphe connexe : Un graphe où il existe un chemin entre chaque paire de sommets.
• Degré d'un sommet : Le nombre d'arêtes incidentes à ce sommet (le nombre d'arêtes qui partent de ce sommet). Dans un graphe orienté, on distingue le degré entrant (nombre d'arêtes arrivant au sommet) et le degré sortant (nombre d'arêtes partant du sommet).

Ce qu'il faut retenir

• Un graphe est une structure composée de sommets et d'arêtes, représentant des relations entre objets.
• Les sommets sont les objets, et les arêtes sont les liens entre ces objets.
• L'ordre d'un graphe est le nombre de ses sommets.
• La taille d'un graphe est le nombre de ses arêtes.
• Bien comprendre ces définitions est essentiel pour étudier les graphes plus en profondeur.