Calcul d'aires sous une courbe : Introduction à l'intégration

Introduction : L'aire sous une courbe

L'aire sous une courbe représente la surface délimitée par la courbe d'une fonction, l'axe des abscisses (l'axe x), et deux bornes verticales (a et b). Comprendre comment calculer cette aire est fondamental en analyse, car elle a des applications dans divers domaines comme la physique (calcul de la distance parcourue), l'économie (calcul du surplus du consommateur), et les statistiques (calcul de probabilités). Imaginez une fonction f(x) représentée graphiquement. L'aire sous cette courbe entre deux points x = a et x = b correspond à la surface 'enfermée' par la courbe, l'axe des x, et les droites verticales x = a et x = b. Notre objectif est de trouver une méthode pour calculer cette surface précisément.

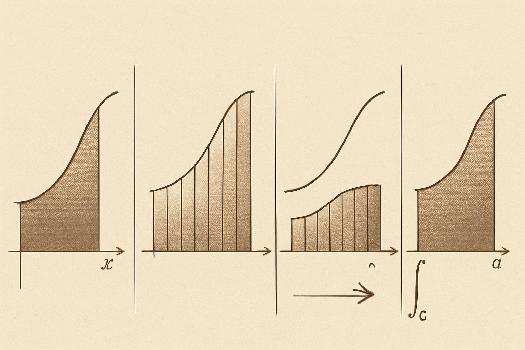
L'approche intuitive : Sommes de Riemann

Une façon intuitive d'approcher l'aire sous une courbe est de la diviser en rectangles. Plus précisément, on découpe l'intervalle [a, b] en n sous-intervalles de largeur égale Δx = (b - a) / n. Ensuite, on construit des rectangles sur chaque sous-intervalle, dont la hauteur est donnée par la valeur de la fonction en un point de ce sous-intervalle. On calcule ensuite la somme des aires de ces rectangles. Cette somme est appelée une somme de Riemann. Il existe différentes manières de choisir le point dans chaque sous-intervalle pour déterminer la hauteur du rectangle :

• Somme de Riemann à gauche : On utilise la valeur de la fonction à l'extrémité gauche de chaque sous-intervalle.
• Somme de Riemann à droite : On utilise la valeur de la fonction à l'extrémité droite de chaque sous-intervalle.
• Somme de Riemann au milieu : On utilise la valeur de la fonction au point milieu de chaque sous-intervalle.

L'intégrale définie : Passage à la limite

L'intégrale définie est une généralisation de la somme de Riemann. Elle est définie comme la limite de la somme de Riemann lorsque le nombre de sous-intervalles (n) tend vers l'infini (ou de manière équivalente, lorsque la largeur des sous-intervalles Δx tend vers zéro). Mathématiquement, l'intégrale définie de f(x) de a à b est notée : ∫_a^b f(x) dx Ici :

• ∫ est le symbole de l'intégrale.
• a et b sont les bornes d'intégration (a est la borne inférieure et b est la borne supérieure).
• f(x) est la fonction à intégrer (appelée intégrande).
• dx indique que l'intégration se fait par rapport à la variable x.

Le théorème fondamental du calcul intégral

Le théorème fondamental du calcul intégral établit un lien crucial entre l'intégration et la dérivation. Il se compose de deux parties, mais la plus pertinente pour le calcul d'aires est la deuxième partie: Si F(x) est une primitive de f(x) (c'est-à-dire, F'(x) = f(x)), alors l'intégrale définie de f(x) de a à b est donnée par : ∫_a^b f(x) dx = F(b) - F(a) En d'autres termes, pour calculer l'aire sous la courbe, il suffit de trouver une primitive de la fonction f(x), d'évaluer cette primitive en les bornes b et a, et de soustraire les deux valeurs obtenues. C'est une méthode beaucoup plus efficace que de calculer directement la limite des sommes de Riemann. Par exemple, si f(x) = x², une primitive est F(x) = (1/3)x³. Pour calculer l'aire sous la courbe de f(x) entre 0 et 2, on calcule F(2) - F(0) = (1/3)(2)³ - (1/3)(0)³ = 8/3. Donc l'aire sous la courbe est 8/3 unités d'aire.

Exemple concret : Calcul de l'aire sous la courbe y = x² entre x = 1 et x = 3

Considérons la fonction f(x) = x². Nous voulons calculer l'aire sous la courbe entre les bornes x = 1 et x = 3. Étape 1: Trouver une primitive de f(x) Une primitive de x² est F(x) = (1/3)x³. (Rappel : la dérivée de (1/3)x³ est bien x²). Étape 2: Évaluer la primitive aux bornes d'intégration Nous devons calculer F(3) et F(1):

• F(3) = (1/3)(3)³ = (1/3)(27) = 9
• F(1) = (1/3)(1)³ = (1/3)(1) = 1/3

Cas particuliers et précautions

• Fonctions négatives : Si f(x) est négative sur une partie de l'intervalle [a, b], l'intégrale définie calculera l'aire 'sous' l'axe des x, qui sera considérée comme négative. Pour calculer l'aire totale (positive), il faut diviser l'intervalle en sections où f(x) est positive et sections où f(x) est négative, calculer les intégrales séparément, et prendre la valeur absolue des intégrales pour les sections où f(x) est négative avant de les additionner.
• Intégrales impropres : Si les bornes d'intégration sont infinies (par exemple, ∫₀^∞ f(x) dx) ou si la fonction f(x) a une singularité (un point où elle n'est pas définie) dans l'intervalle d'intégration, on parle d'intégrale impropre. Le calcul de ces intégrales nécessite des techniques spécifiques de passage à la limite.
• L'importance de la primitive : Le choix de la primitive est crucial. Bien qu'il existe une infinité de primitives pour une même fonction (elles diffèrent par une constante additive), le théorème fondamental du calcul intégral garantit que la différence F(b) - F(a) sera la même quelle que soit la primitive choisie. La constante additive s'annule lors de la soustraction.

Ce qu'il faut retenir

• L'aire sous une courbe : Représente la surface délimitée par la courbe de la fonction, l'axe des abscisses, et les bornes d'intégration.
• Sommes de Riemann : Une approximation de l'aire sous une courbe en la divisant en rectangles.
• Intégrale définie : La limite des sommes de Riemann lorsque le nombre de rectangles tend vers l'infini, donnant l'aire exacte sous la courbe. Notée ∫_a^b f(x) dx.
• Théorème fondamental du calcul intégral : Si F(x) est une primitive de f(x), alors ∫_a^b f(x) dx = F(b) - F(a).
• Calcul pratique : Trouver une primitive de la fonction, l'évaluer aux bornes d'intégration, et soustraire les valeurs.
• Fonctions négatives : L'intégrale calcule l'aire 'sous' l'axe des x comme négative. Prendre la valeur absolue pour obtenir l'aire totale.