Mathématiques > Probabilités et Statistiques > Probabilités > Vocabulaire des probabilités (expérience aléatoire, événement, univers)

Comprendre le vocabulaire de base des probabilités

Introduction aux concepts fondamentaux des probabilités : expérience aléatoire, événement et univers. Des exemples concrets pour une compréhension facile.

Qu'est-ce qu'une expérience aléatoire ?

Une expérience aléatoire est une expérience dont le résultat n'est pas prévisible avec certitude avant sa réalisation. Même si l'expérience est répétée dans les mêmes conditions, le résultat peut varier. Il est important de noter que, bien que l'on ne puisse pas prédire le résultat, on peut souvent connaître l'ensemble des résultats possibles. Exemples :

  • Lancer un dé à six faces : on ne sait pas quel nombre sortira, mais on sait que ce sera un nombre entre 1 et 6.
  • Lancer une pièce de monnaie : on obtient soit pile, soit face, mais on ne peut pas prédire le résultat à l'avance.
  • Tirer une carte d'un jeu de 52 cartes : on ne connaît pas la carte qui sera tirée, mais on sait que ce sera l'une des 52 cartes du jeu.
Contre-exemple :
  • Calculer l'aire d'un carré de côté donné : si on connaît la longueur du côté, on peut déterminer l'aire avec certitude. Ce n'est donc pas une expérience aléatoire.

Définition de l'univers des possibles

L'univers, souvent noté Ω (oméga), est l'ensemble de tous les résultats possibles d'une expérience aléatoire. Chaque élément de l'univers est un résultat élémentaire. Exemples :

  • Lancer un dé à six faces : Ω = {1, 2, 3, 4, 5, 6}.
  • Lancer une pièce de monnaie : Ω = {pile, face}.
  • Tirer une carte d'un jeu de 52 cartes : Ω est l'ensemble de toutes les 52 cartes.
Il est crucial de bien définir l'univers pour pouvoir ensuite étudier les probabilités associées aux différents événements. Par exemple, si on s'intéresse uniquement à savoir si le nombre obtenu au lancer d'un dé est pair ou impair, on peut définir un univers simplifié Ω = {pair, impair}.

Qu'est-ce qu'un événement ?

Un événement est un sous-ensemble de l'univers. Autrement dit, c'est un ensemble de résultats possibles de l'expérience aléatoire. Exemples :

  • Lancer un dé : l'événement "obtenir un nombre pair" est l'ensemble {2, 4, 6}.
  • Lancer une pièce de monnaie : l'événement "obtenir pile" est l'ensemble {pile}.
  • Tirer une carte d'un jeu : l'événement "tirer un as" est l'ensemble des quatre as du jeu.
Un événement peut être :
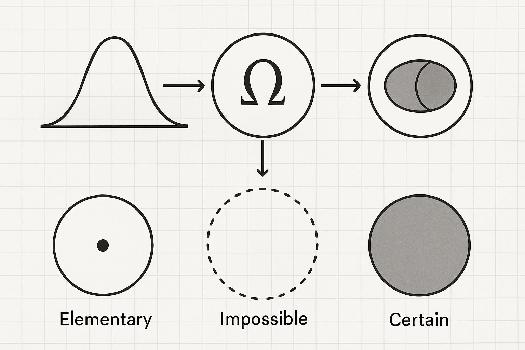
  • Élémentaire : il ne contient qu'un seul résultat (ex : obtenir 3 en lançant un dé).
  • Impossible : il ne contient aucun résultat (ex : obtenir 7 en lançant un dé à 6 faces). On le note ∅ (ensemble vide).
  • Certain : il contient tous les résultats possibles (ex : obtenir un nombre entre 1 et 6 en lançant un dé à 6 faces). Il est égal à l'univers Ω.
On peut effectuer des opérations sur les événements, comme l'union (A ∪ B : A ou B se réalise), l'intersection (A ∩ B : A et B se réalisent) et le complémentaire (Ā : A ne se réalise pas).

Ce qu'il faut retenir

  • Expérience aléatoire : expérience dont le résultat est incertain.
  • Univers (Ω) : ensemble de tous les résultats possibles d'une expérience aléatoire.
  • Événement : sous-ensemble de l'univers, représentant un ensemble de résultats possibles.
  • Événement élémentaire: un événement contenant un seul résultat.
  • Événement impossible: un événement ne contenant aucun résultat.
  • Événement certain: un événement contenant tous les résultats.
Comprendre ces définitions est essentiel pour aborder l'étude des probabilités.

← Comprendre la Probabilité d'un Événement Espérance, Variance et Écart-type : Variables Aléatoires Discrètes →

FAQ

  • Quelle est la différence entre une expérience aléatoire et une expérience déterministe ?

    Dans une expérience aléatoire, le résultat est incertain avant sa réalisation. Dans une expérience déterministe, le résultat est prévisible avec certitude si les conditions initiales sont connues.
  • L'univers doit-il toujours être fini ?

    Non, l'univers peut être fini (ex : lancer un dé), infini dénombrable (ex : nombre de lancers d'une pièce jusqu'à obtenir pile) ou infini non dénombrable (ex : choisir un nombre réel entre 0 et 1).
  • Comment représenter un événement ?

    Un événement peut être représenté par une phrase décrivant les résultats qui le composent, ou par l'ensemble des résultats lui-même. Par exemple, l'événement "obtenir un nombre pair en lançant un dé" peut être représenté par la phrase ou par l'ensemble {2, 4, 6}.