Factorisation et racines des polynômes : Techniques et applications

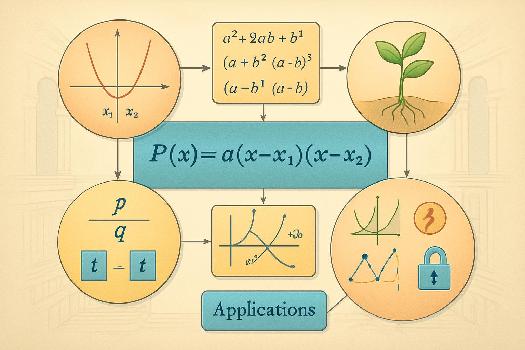
Lien entre factorisation et racines

La factorisation d'un polynôme et la recherche de ses racines sont deux problèmes intimement liés. Si on connaît une factorisation d'un polynôme, il est facile de trouver ses racines, et inversement, si on connaît toutes les racines d'un polynôme, on peut le factoriser (à un facteur constant près). Plus précisément, si P(x) est un polynôme de degré n, et que x₁, x₂, ..., x_n sont ses racines (comptées avec multiplicité), alors on peut factoriser P(x) sous la forme : P(x) = a(x - x₁)(x - x₂)...(x - x_n) où a est le coefficient dominant de P(x) (c'est-à-dire le coefficient du terme de plus haut degré).

Techniques de factorisation avancées

Au-delà des méthodes de factorisation de base (factorisation par mise en évidence, factorisation des trinômes du second degré, etc.), il existe des techniques plus avancées pour factoriser des polynômes :

• Utilisation des identités remarquables : Certaines identités remarquables (comme a² - b² = (a - b)(a + b) ou a³ - b³ = (a - b)(a² + ab + b²)) peuvent être utilisées pour factoriser des polynômes de formes spécifiques.
• Regroupement de termes : On peut parfois factoriser un polynôme en regroupant ses termes de manière appropriée pour faire apparaître un facteur commun.
• Substitution : On peut parfois simplifier un polynôme en effectuant une substitution de variable. Par exemple, si on a un polynôme en x⁴ et x², on peut poser y = x² pour obtenir un polynôme du second degré en y, que l'on peut factoriser plus facilement.
• Théorème des racines rationnelles : Ce théorème permet de trouver les racines rationnelles potentielles d'un polynôme à coefficients entiers. Si P(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀ est un polynôme à coefficients entiers, alors toute racine rationnelle p/q (où p et q sont des entiers premiers entre eux) de P(x) doit vérifier que p est un diviseur de a₀ et que q est un diviseur de a_n.

Exemple détaillé : Utilisation du théorème des racines rationnelles

Considérons le polynôme P(x) = 2x³ - 3x² - 3x + 2. On veut trouver ses racines rationnelles en utilisant le théorème des racines rationnelles.

• Les diviseurs de a₀ = 2 sont ±1 et ±2.
• Les diviseurs de a_n = 2 sont ±1 et ±2.

Donc, les racines rationnelles potentielles sont ±1, ±2, ±1/2. Testons ces valeurs :

• P(1) = 2 - 3 - 3 + 2 = -2 ≠ 0
• P(-1) = -2 - 3 + 3 + 2 = 0. Donc, -1 est une racine.

Puisque -1 est une racine, on peut diviser P(x) par (x + 1) pour obtenir un polynôme de degré 2 : 2x³ - 3x² - 3x + 2 = (x + 1)(2x² - 5x + 2) On peut ensuite factoriser le polynôme du second degré : 2x² - 5x + 2 = (2x - 1)(x - 2) Donc, les racines de P(x) sont -1, 1/2 et 2.

Applications de la factorisation et des racines

La factorisation et la recherche des racines des polynômes ont de nombreuses applications en mathématiques, en physique, en ingénierie et dans d'autres domaines :

• Résolution d'équations polynomiales : Trouver les racines d'un polynôme est équivalent à résoudre l'équation polynomiale P(x) = 0.
• Étude du signe d'un polynôme : La connaissance des racines d'un polynôme permet de déterminer les intervalles où le polynôme est positif ou négatif.
• Modélisation de phénomènes physiques : Les polynômes sont souvent utilisés pour modéliser des phénomènes physiques, comme le mouvement d'un projectile ou la croissance d'une population. La recherche des racines permet d'analyser le comportement de ces modèles.
• Interpolation polynomiale : On peut utiliser un polynôme pour interpoler un ensemble de données. La factorisation peut aider à simplifier l'expression du polynôme interpolateur.
• Cryptographie : Les polynômes sont utilisés dans certaines techniques de cryptographie pour chiffrer et déchiffrer des messages.

Ce qu'il faut retenir

• Lien factorisation-racines : P(x) = a(x - x₁)(x - x₂)...(x - x_n)
• Techniques avancées de factorisation : Identités remarquables, regroupement de termes, substitution, théorème des racines rationnelles.
• Théorème des racines rationnelles : p/q est une racine potentielle si p divise a₀ et q divise a_n.
• Applications : Résolution d'équations, étude du signe, modélisation, interpolation, cryptographie.