Le Cercle Trigonométrique: Découverte et Applications

Définition et Construction du Cercle Trigonométrique

Le cercle trigonométrique est un cercle de rayon 1 centré à l'origine d'un repère orthonormé. Son équation est x² + y² = 1. Il est fondamental en trigonométrie car il permet de visualiser les fonctions trigonométriques pour tous les angles, et pas seulement les angles aigus d'un triangle rectangle. Pour le construire:

1. Tracez un repère orthonormé (O, I, J).
2. Tracez un cercle de centre O et de rayon 1. Le point I a pour coordonnées (1, 0).

Angles et Mesures sur le Cercle Trigonométrique

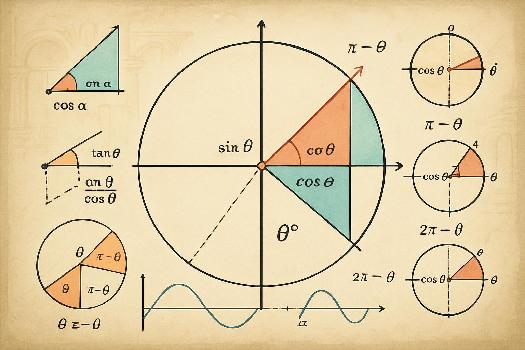
Chaque point M sur le cercle trigonométrique est associé à un angle θ (thêta) formé par l'axe des abscisses (OI) et le rayon OM. L'angle θ est mesuré en radians. Un angle positif est mesuré dans le sens trigonométrique (sens inverse des aiguilles d'une montre), tandis qu'un angle négatif est mesuré dans le sens horaire. Plusieurs angles peuvent correspondre au même point M, car si θ correspond à M, alors θ + 2πk (où k est un entier relatif) correspond également à M. Par exemple, π/2, 5π/2, -3π/2 correspondent tous au même point sur le cercle trigonométrique.

Sinus et Cosinus d'un Angle

Le cosinus d'un angle θ, noté cos(θ), est l'abscisse du point M associé à l'angle θ sur le cercle trigonométrique. Le sinus d'un angle θ, noté sin(θ), est l'ordonnée du point M associé à l'angle θ sur le cercle trigonométrique. Ainsi, les coordonnées du point M sont (cos(θ), sin(θ)). Étant donné que le rayon du cercle trigonométrique est 1, on a toujours -1 ≤ cos(θ) ≤ 1 et -1 ≤ sin(θ) ≤ 1. De plus, on a la relation fondamentale: cos²(θ) + sin²(θ) = 1 (provenant du théorème de Pythagore).

Voici quelques valeurs remarquables:

• cos(0) = 1, sin(0) = 0
• cos(π/2) = 0, sin(π/2) = 1
• cos(π) = -1, sin(π) = 0
• cos(3π/2) = 0, sin(3π/2) = -1

Tangente d'un Angle

La tangente d'un angle θ, notée tan(θ), est définie comme le rapport du sinus au cosinus: tan(θ) = sin(θ) / cos(θ). Graphiquement, la tangente est l'ordonnée du point d'intersection de la droite (OM) avec la droite verticale passant par le point I (d'abscisse 1). La tangente n'est pas définie lorsque cos(θ) = 0, c'est-à-dire pour θ = π/2 + kπ, où k est un entier relatif. La tangente peut prendre n'importe quelle valeur réelle (contrairement au sinus et au cosinus qui sont bornés entre -1 et 1).

Valeurs remarquables:

• tan(0) = 0
• tan(π/4) = 1
• tan(π/3) = √3

Angles Associés et Propriétés de Symétrie

Le cercle trigonométrique permet de visualiser facilement les relations entre les fonctions trigonométriques pour des angles associés.

• Angles opposés: cos(-θ) = cos(θ) et sin(-θ) = -sin(θ). Le cosinus est une fonction paire, et le sinus est une fonction impaire.
• Angles supplémentaires: cos(π - θ) = -cos(θ) et sin(π - θ) = sin(θ).
• Angles complémentaires: cos(π/2 - θ) = sin(θ) et sin(π/2 - θ) = cos(θ).
• Angles θ + π: cos(θ + π) = -cos(θ) et sin(θ + π) = -sin(θ).

Résolution d'Équations Trigonométriques

Le cercle trigonométrique est un outil précieux pour résoudre des équations trigonométriques. Par exemple, pour résoudre l'équation cos(x) = a (où -1 ≤ a ≤ 1), on recherche les points sur le cercle trigonométrique dont l'abscisse est égale à a. Il y a généralement deux solutions dans l'intervalle [0, 2π[, et toutes les autres solutions s'obtiennent en ajoutant des multiples de 2π. De même, pour résoudre sin(x) = b (où -1 ≤ b ≤ 1), on recherche les points sur le cercle trigonométrique dont l'ordonnée est égale à b. Pour résoudre tan(x) = c (où c est un nombre réel), on trace la droite verticale d'équation x = 1 et on cherche le point d'intersection avec la droite passant par l'origine et de coefficient directeur c.

Applications

Les fonctions trigonométriques sont utilisées dans de nombreux domaines:

• Physique: Description des oscillations, des ondes, des mouvements périodiques.
• Ingénierie: Analyse des circuits électriques, conception de structures.
• Navigation: Calcul de distances et de directions.
• Informatique: Graphismes 3D, traitement du signal.

Ce qu'il faut retenir

• Définition: Le cercle trigonométrique est un cercle de rayon 1 centré à l'origine d'un repère orthonormé.
• Angles: Les angles sont mesurés en radians, un tour complet valant 2π radians.
• Sinus et Cosinus: Le cosinus d'un angle est l'abscisse du point correspondant sur le cercle, et le sinus est son ordonnée. cos²(θ) + sin²(θ) = 1.
• Tangente: tan(θ) = sin(θ) / cos(θ).
• Angles Associés: Connaître les relations entre les angles opposés, supplémentaires, complémentaires, etc.
• Résolution d'Équations: Utiliser le cercle pour trouver les solutions des équations trigonométriques.