Les Fonctions Inverses : Un Guide Complet

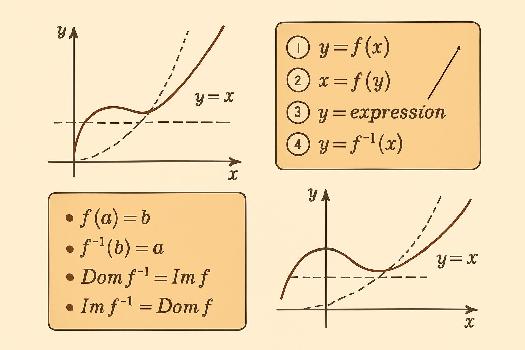
Introduction aux Fonctions Inverses

En mathématiques, une fonction inverse est une fonction qui « défait » l'action d'une autre fonction. Autrement dit, si une fonction f prend une entrée x et produit une sortie y, alors la fonction inverse de f, notée f^-1, prend y comme entrée et produit x comme sortie.

Exemple simple :

Considérons la fonction f(x) = x + 2. Pour trouver sa fonction inverse, on cherche une fonction qui, lorsqu'elle est appliquée au résultat de f(x), nous redonne x. Dans ce cas, la fonction inverse est f^-1(y) = y - 2.

Si on prend x = 3, alors f(3) = 3 + 2 = 5. Ensuite, f^-1(5) = 5 - 2 = 3, ce qui nous ramène à notre valeur de départ.

Comment Déterminer la Fonction Inverse

Voici les étapes générales pour trouver la fonction inverse d'une fonction f(x) :

1. Remplacer f(x) par y. Cela facilite la manipulation de l'équation.
2. Échanger x et y. Cette étape est cruciale, car elle reflète l'inversion de la fonction.
3. Résoudre pour y en termes de x. Isolez y d'un côté de l'équation.
4. Remplacer y par f^-1(x). Ceci indique que vous avez trouvé la fonction inverse.

Exemple :

Trouvons la fonction inverse de f(x) = 3x - 1.

1. y = 3x - 1
2. x = 3y - 1
3. x + 1 = 3y => y = (x + 1) / 3
4. f^-1(x) = (x + 1) / 3

Représentation Graphique des Fonctions Inverses

Le graphique d'une fonction inverse est une réflexion du graphique de la fonction originale par rapport à la droite y = x. Cela signifie que si le point (a, b) se trouve sur le graphique de f(x), alors le point (b, a) se trouve sur le graphique de f^-1(x).

Pour visualiser cela, imaginez plier le graphique le long de la droite y = x. Le graphique de la fonction originale et celui de sa fonction inverse se superposeront.

Exemple :

Si le point (2, 5) est sur le graphique de f(x), alors le point (5, 2) est sur le graphique de f^-1(x).

Domaine et Image des Fonctions Inverses

Le domaine d'une fonction inverse est l'image de la fonction originale, et l'image de la fonction inverse est le domaine de la fonction originale. En d'autres termes :

• Dom(f^-1) = Im(f)
• Im(f^-1) = Dom(f)

Comprendre cette relation est essentiel pour déterminer si une fonction a une inverse et pour comprendre les limitations de la fonction inverse.

Exemple :

Si f(x) = √x (racine carrée de x), alors Dom(f) = [0, ∞) et Im(f) = [0, ∞). La fonction inverse est f^-1(x) = x², mais avec un domaine restreint [0, ∞). Sans cette restriction, x² ne serait pas l'inverse de √x.

Fonctions non inversibles

Toutes les fonctions n'ont pas une inverse. Une fonction doit être bijective (à la fois injective et surjective) pour avoir une inverse. En termes simples, une fonction est injective si chaque élément de son image a au plus un antécédent, et elle est surjective si son image est égale à son ensemble d'arrivée.

Une façon de vérifier si une fonction est injective est d'utiliser le test de la droite horizontale. Si une droite horizontale coupe le graphique de la fonction en plus d'un point, alors la fonction n'est pas injective et n'a pas d'inverse.

Exemple :

La fonction f(x) = x² n'est pas injective car f(2) = 4 et f(-2) = 4. Par conséquent, elle n'a pas d'inverse sur l'ensemble des nombres réels. Cependant, si nous restreignons le domaine à [0, ∞), elle devient injective et admet une inverse, qui est f^-1(x) = √x.

Exemples avancés et cas particuliers

• Fonctions trigonométriques inverses : Les fonctions trigonométriques (sinus, cosinus, tangente, etc.) ont des inverses définies sur des intervalles restreints pour garantir qu'elles soient bijectives. Par exemple, l'inverse de sinus (arcsinus) est définie sur l'intervalle [-1, 1] et son image est [-π/2, π/2].
• Fonctions exponentielles et logarithmiques inverses : La fonction exponentielle f(x) = e^x a pour inverse la fonction logarithme naturel f^-1(x) = ln(x). Ces fonctions sont essentielles dans de nombreux domaines des mathématiques et des sciences.

Ce qu'il faut retenir

• Définition : Une fonction inverse « défait » l'action de la fonction originale. Si f(a) = b, alors f^-1(b) = a.
• Étapes pour trouver l'inverse :
  1. Remplacer f(x) par y.
  2. Échanger x et y.
  3. Résoudre pour y.
  4. Remplacer y par f^-1(x).
• Graphique : Le graphique de la fonction inverse est une réflexion du graphique de la fonction originale par rapport à la droite y = x.
• Domaine et Image : Dom(f^-1) = Im(f) et Im(f^-1) = Dom(f).
• Bijectivité : Une fonction doit être bijective pour avoir une inverse. Utilisez le test de la droite horizontale pour vérifier l'injectivité.