Mathématiques > Algèbre > Fonctions > Représentation graphique d'une fonction

Transformations de Graphiques de Fonctions

Découvrez comment les transformations géométriques (translation, réflexion, étirement, compression) affectent le graphique d'une fonction. Apprenez à appliquer ces transformations et à prédire l'allure du graphique résultant.

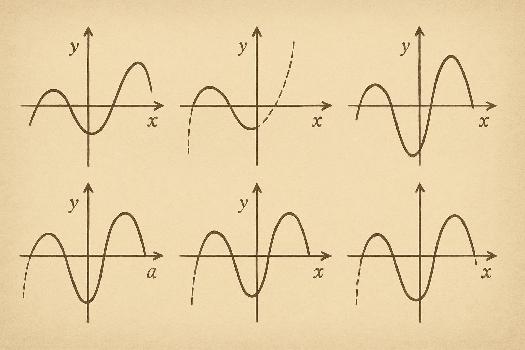
Introduction aux Transformations

Les transformations de fonctions permettent de modifier un graphique de fonction de base pour obtenir de nouvelles fonctions. Les transformations courantes incluent les translations, les réflexions, les étirements et les compressions.

Comprendre ces transformations vous permet de prédire l'allure du graphique d'une fonction transformée sans avoir à la tracer point par point.

Translations Verticales

Une translation verticale déplace le graphique vers le haut ou vers le bas. Si c est une constante positive, alors:

  • f(x) + c déplace le graphique de f(x) vers le haut de c unités.
  • f(x) - c déplace le graphique de f(x) vers le bas de c unités.

Exemple: Si f(x) = x2, alors f(x) + 2 = x2 + 2 déplace la parabole vers le haut de 2 unités.

Translations Horizontales

Une translation horizontale déplace le graphique vers la gauche ou vers la droite. Si c est une constante positive, alors:

  • f(x - c) déplace le graphique de f(x) vers la droite de c unités.
  • f(x + c) déplace le graphique de f(x) vers la gauche de c unités.

Attention: Le signe est inversé par rapport à l'intuition. f(x - 2) déplace le graphique vers la droite de 2 unités.

Exemple: Si f(x) = x2, alors f(x - 3) = (x - 3)2 déplace la parabole vers la droite de 3 unités.

Réflexions

Une réflexion inverse le graphique par rapport à un axe:

  • -f(x) reflète le graphique de f(x) par rapport à l'axe des x.
  • f(-x) reflète le graphique de f(x) par rapport à l'axe des y.

Exemple: Si f(x) = √x, alors -f(x) = -√x reflète la courbe par rapport à l'axe des x, et f(-x) = √(-x) reflète la courbe par rapport à l'axe des y.

Étirements et Compressions Verticaux

Un étirement ou une compression vertical modifie la hauteur du graphique:

  • Si k > 1, alors k * f(x) étire le graphique de f(x) verticalement d'un facteur de k.
  • Si 0 < k < 1, alors k * f(x) comprime le graphique de f(x) verticalement d'un facteur de k.

Exemple: Si f(x) = x2, alors 2 * f(x) = 2x2 étire la parabole verticalement d'un facteur de 2, et 0.5 * f(x) = 0.5x2 la comprime verticalement d'un facteur de 0.5.

Étirements et Compressions Horizontaux

Un étirement ou une compression horizontal modifie la largeur du graphique:

  • Si k > 1, alors f(kx) comprime le graphique de f(x) horizontalement d'un facteur de k.
  • Si 0 < k < 1, alors f(kx) étire le graphique de f(x) horizontalement d'un facteur de k.

Attention: Encore une fois, le comportement est inversé par rapport à l'intuition.

Exemple: Si f(x) = sin(x), alors f(2x) = sin(2x) comprime la sinusoïde horizontalement, doublant sa fréquence, et f(0.5x) = sin(0.5x) l'étire horizontalement, divisant sa fréquence par deux.

Combinaison de Transformations

Il est possible d'appliquer plusieurs transformations à une même fonction. L'ordre des transformations est important.

Conseil: Appliquez les étirements/compressions en premier, puis les réflexions, puis les translations. Il est souvent utile d'écrire les étapes de transformations avec des équations intermédiaires.

Ce qu'il faut retenir

  • Les translations verticales ajoutent ou soustraient une constante à la fonction (f(x) + c ou f(x) - c).
  • Les translations horizontales ajoutent ou soustraient une constante à la variable indépendante (f(x + c) ou f(x - c)).
  • Les réflexions inversent le graphique par rapport à un axe (-f(x) ou f(-x)).
  • Les étirements et compressions verticaux multiplient la fonction par une constante (k * f(x)).
  • Les étirements et compressions horizontaux multiplient la variable indépendante par une constante (f(kx)).
  • L'ordre d'application des transformations est important.

← Suites Géométriques : Comprendre et Maîtriser Utilisation du Tableau de Signe pour les Inéquations du Second Degré →

FAQ

  • Comment puis-je me souvenir de la direction des translations horizontales?

    Pensez que f(x - c) déplace le graphique vers la droite parce que vous devez ajouter c à chaque valeur de x pour obtenir la même valeur de f(x).
  • Est-ce que l'ordre des transformations importe toujours?

    Oui, l'ordre des transformations est crucial. Changez l'ordre et vous obtiendrez un graphique différent. Il est généralement plus sûr d'appliquer les étirements/compressions avant les translations.