Mathématiques > Analyse > Intégration > Propriétés de l'intégrale

Linéarité et Additivité de l'Intégrale

Explorez en détail les propriétés fondamentales de linéarité et d'additivité de l'intégrale définie, avec des exemples concrets et des applications pour les élèves de lycée.

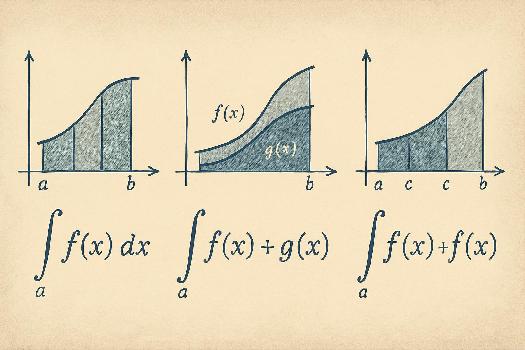
Introduction

Bienvenue dans cette exploration des propriétés de l'intégrale définie. Nous allons nous concentrer sur deux propriétés essentielles : la linéarité et l'additivité. Ces propriétés sont cruciales pour simplifier le calcul d'intégrales complexes et pour comprendre les fondements de l'intégration.

Linéarité de l'Intégrale

La linéarité de l'intégrale se décompose en deux sous-propriétés : l'intégrale d'une fonction multipliée par une constante, et l'intégrale d'une somme de fonctions.

1. Intégrale d'une fonction multipliée par une constante :
Pour toute constante k et toute fonction f(x) intégrable sur un intervalle [a, b], nous avons :

∫ab k * f(x) dx = k * ∫ab f(x) dx

Cela signifie que l'on peut sortir une constante multiplicative de l'intégrale.

Exemple :
Calculons ∫01 3x2 dx. On sait que ∫01 x2 dx = [x3/3]01 = 1/3.
Donc, ∫01 3x2 dx = 3 * ∫01 x2 dx = 3 * (1/3) = 1.

2. Intégrale d'une somme de fonctions :
Pour deux fonctions f(x) et g(x) intégrables sur un intervalle [a, b], nous avons :

∫ab [f(x) + g(x)] dx = ∫ab f(x) dx + ∫ab g(x) dx

Cela signifie que l'on peut séparer l'intégrale d'une somme en la somme des intégrales.

Exemple :
Calculons ∫02 (x + x2) dx. Nous pouvons séparer cette intégrale en deux :
∫02 x dx + ∫02 x2 dx.
Nous savons que ∫02 x dx = [x2/2]02 = 2 et ∫02 x2 dx = [x3/3]02 = 8/3.
Donc, ∫02 (x + x2) dx = 2 + 8/3 = 14/3.

Additivité de l'Intégrale par Rapport à l'Intervalle d'Intégration

Si f(x) est une fonction intégrable sur un intervalle [a, b], et si c est un point entre a et b (c'est-à-dire a < c < b), alors nous avons :

∫ab f(x) dx = ∫ac f(x) dx + ∫cb f(x) dx

Cette propriété est très utile pour diviser une intégrale sur un intervalle en plusieurs intégrales sur des sous-intervalles, notamment lorsque la fonction a des comportements différents sur différentes parties de l'intervalle.

Exemple :
Supposons que nous voulions calculer l'intégrale de |x| de -1 à 2. Puisque |x| = -x pour x < 0 et |x| = x pour x ≥ 0, nous pouvons diviser l'intégrale en deux parties :

∫-12 |x| dx = ∫-10 -x dx + ∫02 x dx

∫-10 -x dx = [-x2/2]-10 = 0 - (-1/2) = 1/2
∫02 x dx = [x2/2]02 = 2 - 0 = 2

Donc, ∫-12 |x| dx = 1/2 + 2 = 5/2.

Convention d'Intégration

Il est important de noter la convention suivante :

∫aa f(x) dx = 0

Et si nous inversons les bornes d'intégration :

∫ba f(x) dx = - ∫ab f(x) dx

Ces conventions sont nécessaires pour assurer la cohérence des propriétés de l'intégrale, en particulier l'additivité.

Ce qu'il faut retenir

Voici les points clés à retenir sur les propriétés de l'intégrale :

  • Linéarité : ∫ab k * f(x) dx = k * ∫ab f(x) dx et ∫ab [f(x) + g(x)] dx = ∫ab f(x) dx + ∫ab g(x) dx
  • Additivité par rapport à l'intervalle : ∫ab f(x) dx = ∫ac f(x) dx + ∫cb f(x) dx (si a < c < b)
  • Convention : ∫aa f(x) dx = 0 et ∫ba f(x) dx = - ∫ab f(x) dx

Ces propriétés sont des outils puissants pour simplifier et calculer des intégrales. N'oubliez pas de les utiliser à bon escient !

← La Fonction Logarithme Népérien : Un Guide Complet Nombre dérivé et tangente : Cours et exercices →

FAQ

  • Quand est-il utile d'utiliser la propriété d'additivité par rapport à l'intervalle ?

    La propriété d'additivité est particulièrement utile lorsque la fonction que vous intégrez est définie par morceaux, ou lorsque son comportement change radicalement à un certain point de l'intervalle d'intégration. L'exemple de la fonction valeur absolue est un excellent cas d'utilisation.
  • Peut-on utiliser la linéarité avec plus de deux fonctions additionnées ?

    Oui, la propriété de linéarité s'étend à un nombre quelconque de fonctions. Par exemple, ∫ab [f(x) + g(x) + h(x)] dx = ∫ab f(x) dx + ∫ab g(x) dx + ∫ab h(x) dx.