Calcul de Volumes par Intégration

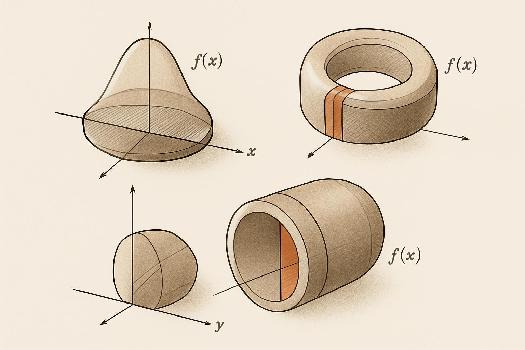
Introduction au Calcul de Volumes par Intégration

Le calcul de volumes par intégration est une application puissante de l'intégrale définie. Au lieu de calculer l'aire sous une courbe, on calcule le volume d'un solide. L'idée de base est de diviser le solide en tranches fines, d'approximer le volume de chaque tranche, puis de sommer ces volumes en utilisant une intégrale. Ce processus est particulièrement utile pour les solides dont la forme n'est pas simple et ne peut pas être facilement calculée avec des formules géométriques standards.

Méthode des Disques

La méthode des disques est utilisée pour calculer le volume d'un solide de révolution, c'est-à-dire un solide obtenu en faisant tourner une région plane autour d'un axe. Imaginez que vous faites tourner une courbe y = f(x) autour de l'axe des x.

Étapes:

1. Divisez l'intervalle [a, b] sur l'axe des x en n petits sous-intervalles de largeur Δx.
2. Pour chaque sous-intervalle, considérez un disque dont le rayon est f(x) et l'épaisseur est Δx. Le volume de ce disque est approximativement π[f(x)]²Δx.
3. Sommez les volumes de tous les disques et prenez la limite lorsque Δx tend vers zéro. Cela donne l'intégrale définie: V = ∫[a, b] π[f(x)]² dx

Méthode des Anneaux (Rondelles)

La méthode des anneaux (ou rondelles) est une extension de la méthode des disques. Elle est utilisée lorsque le solide de révolution a un trou en son centre. Imaginez que vous faites tourner une région bornée par deux courbes, y = f(x) et y = g(x), autour de l'axe des x, où f(x) ≥ g(x) pour tout x dans [a, b].

Étapes:

1. Divisez l'intervalle [a, b] sur l'axe des x en n petits sous-intervalles de largeur Δx.
2. Pour chaque sous-intervalle, considérez un anneau dont le rayon extérieur est f(x), le rayon intérieur est g(x) et l'épaisseur est Δx. Le volume de cet anneau est approximativement π([f(x)]² - [g(x)]²)Δx.
3. Sommez les volumes de tous les anneaux et prenez la limite lorsque Δx tend vers zéro. Cela donne l'intégrale définie: V = ∫[a, b] π([f(x)]² - [g(x)]²) dx

Méthode des Coquilles Cylindriques

La méthode des coquilles cylindriques est une technique alternative pour calculer le volume d'un solide de révolution. Au lieu de découper le solide en disques ou anneaux perpendiculaires à l'axe de rotation, on le découpe en coquilles cylindriques parallèles à l'axe de rotation.

Étapes :

1. Divisez l'intervalle sur l'axe des x (ou y, selon l'axe de rotation) en n petits sous-intervalles de largeur Δx.
2. Pour chaque sous-intervalle, considérez une coquille cylindrique dont le rayon est x (la distance à l'axe de rotation), la hauteur est f(x) (la hauteur de la courbe) et l'épaisseur est Δx. Le volume de cette coquille est approximativement 2πx f(x) Δx.
3. Sommez les volumes de toutes les coquilles et prenez la limite lorsque Δx tend vers zéro. Cela donne l'intégrale définie : V = ∫[a, b] 2πx f(x) dx

Choix de la Méthode Appropriée

Le choix de la méthode (disques, anneaux ou coquilles cylindriques) dépend de la géométrie du solide et de l'axe de rotation. En général:

• Si l'axe de rotation est horizontal et que la fonction est définie en termes de x, la méthode des disques ou des anneaux est souvent plus simple.
• Si l'axe de rotation est vertical et que la fonction est définie en termes de x, la méthode des coquilles cylindriques peut être plus avantageuse.
• Il est parfois possible d'utiliser les deux méthodes, mais l'une peut être plus facile à calculer que l'autre.

Ce qu'il faut retenir

• Méthode des Disques : Pour les solides de révolution sans trou, V = ∫[a, b] π[f(x)]² dx (rotation autour de l'axe des x).
• Méthode des Anneaux : Pour les solides de révolution avec un trou, V = ∫[a, b] π([f(x)]² - [g(x)]²) dx (rotation autour de l'axe des x).
• Méthode des Coquilles Cylindriques : Alternative pour les solides de révolution, souvent utile lorsque l'axe de rotation est vertical, V = ∫[a, b] 2πx f(x) dx (rotation autour de l'axe des y).
• Il est essentiel de bien visualiser le solide et de choisir la méthode appropriée pour simplifier le calcul de l'intégrale. Dessiner le solide peut être très utile.