Mathématiques > Analyse > Intégration > Calcul d'aires sous une courbe

Calcul d'aires : Techniques avancées et applications

Explorez des techniques avancées pour le calcul d'aires, incluant l'intégration par parties, le changement de variable, et le calcul d'aires entre deux courbes. Des exemples détaillés pour les élèves de lycée.

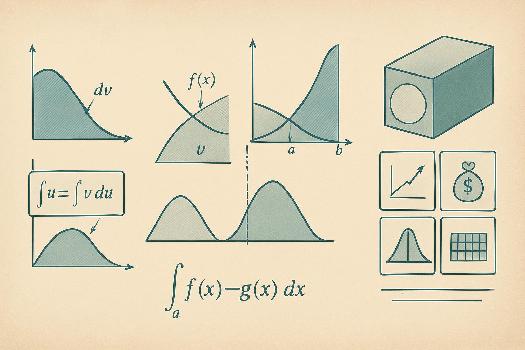
Intégration par parties

L'intégration par parties est une technique utile pour intégrer des produits de fonctions. Elle découle de la règle de dérivation d'un produit de fonctions (uv)' = u'v + uv'. La formule d'intégration par parties est : ∫ u dv = uv - ∫ v du Où u et v sont des fonctions de x, et du et dv sont leurs différentielles respectives. La clé de l'utilisation de cette méthode est de choisir judicieusement les fonctions u et dv. L'objectif est de simplifier l'intégrale ∫ v du par rapport à l'intégrale originale ∫ u dv. En général, on choisit u comme la fonction qui se simplifie lorsqu'on la dérive, et dv comme le reste de l'intégrande (incluant dx). Exemple : Calculer ∫ x cos(x) dx

  • On pose u = x et dv = cos(x) dx
  • Alors du = dx et v = ∫ cos(x) dx = sin(x)
  • En appliquant la formule d'intégration par parties :
  • ∫ x cos(x) dx = x sin(x) - ∫ sin(x) dx = x sin(x) + cos(x) + C (où C est la constante d'intégration)
L'intégration par parties est particulièrement utile pour intégrer des fonctions comme x*ex, x*ln(x), ou des produits de fonctions trigonométriques et de polynômes.

Changement de variable (Substitution)

Le changement de variable, aussi appelé substitution, est une technique qui simplifie l'intégration en remplaçant une partie de l'intégrande par une nouvelle variable. L'objectif est de transformer l'intégrale en une forme plus simple à intégrer. Méthode générale :

  • Choisir une substitution appropriée u = g(x), où g(x) est une partie de l'intégrande.
  • Calculer la différentielle du = g'(x) dx.
  • Exprimer dx en fonction de du : dx = du / g'(x).
  • Substituer u et dx dans l'intégrale originale.
  • Calculer la nouvelle intégrale en termes de u.
  • Remplacer u par g(x) pour exprimer le résultat final en termes de x.
Exemple : Calculer ∫ 2x (x2 + 1)3 dx
  • On pose u = x2 + 1
  • Alors du = 2x dx
  • L'intégrale devient ∫ u3 du = (1/4)u4 + C
  • En remplaçant u par x2 + 1, on obtient (1/4)(x2 + 1)4 + C
Le changement de variable est crucial pour intégrer des fonctions composées ou des expressions qui se simplifient avec une substitution adéquate. Bien identifier la substitution est primordiale.

Calcul d'aires entre deux courbes

Pour calculer l'aire entre deux courbes f(x) et g(x) sur un intervalle [a, b], où f(x) ≥ g(x) pour tout x dans [a, b], on calcule l'intégrale de la différence entre les deux fonctions : Aire = ∫ab [f(x) - g(x)] dx Intuitivement, on soustrait l'aire sous la courbe g(x) de l'aire sous la courbe f(x). Si f(x) et g(x) se croisent plusieurs fois dans l'intervalle [a, b], il faut diviser l'intervalle en sous-intervalles où soit f(x) ≥ g(x), soit g(x) ≥ f(x), et calculer l'intégrale sur chaque sous-intervalle séparément en prenant la valeur absolue du résultat pour chaque sous-intervalle avant de les additionner. Cela garantit que l'aire totale est positive. Exemple : Calculer l'aire entre y = x2 et y = x sur l'intervalle [0, 1]

  • Sur l'intervalle [0, 1], x ≥ x2.
  • L'aire est donnée par ∫01 (x - x2) dx = [x2/2 - x3/3]01 = (1/2 - 1/3) - (0 - 0) = 1/6.
L'aire entre les deux courbes est de 1/6 unités d'aire.

Applications du calcul d'aires

Le calcul d'aires a de nombreuses applications dans diverses disciplines :

  • Physique : Calcul de la distance parcourue par un objet en intégrant sa vitesse en fonction du temps. Calcul du travail effectué par une force en intégrant la force en fonction de la distance.
  • Économie : Calcul du surplus du consommateur et du producteur. L'aire représente le bénéfice économique supplémentaire que les consommateurs et les producteurs reçoivent de l'échange de biens ou de services.
  • Statistiques et probabilités : L'aire sous une courbe de densité de probabilité représente la probabilité qu'une variable aléatoire prenne une valeur dans un certain intervalle.
  • Ingénierie : Calcul du volume d'un solide de révolution en intégrant l'aire de ses sections transversales.
Ces applications démontrent la puissance et l'importance du calcul d'aires dans la résolution de problèmes concrets.

Ce qu'il faut retenir

  • Intégration par parties : ∫ u dv = uv - ∫ v du. Choisir u et dv judicieusement pour simplifier l'intégrale.
  • Changement de variable (Substitution) : Remplacer une partie de l'intégrande par une nouvelle variable pour simplifier l'intégration.
  • Aire entre deux courbes : ∫ab [f(x) - g(x)] dx, où f(x) ≥ g(x) sur [a, b]. Diviser l'intervalle si les courbes se croisent et prendre la valeur absolue des intégrales.
  • Applications : Physique (distance, travail), économie (surplus), statistiques (probabilités), ingénierie (volumes).

← Calcul Pratique des Limites: Exemples et Techniques Calcul d'aires sous une courbe : Introduction à l'intégration →

FAQ

  • Comment choisir u et dv lors de l'intégration par parties ?

    Choisir u comme la fonction qui se simplifie en dérivant et dv comme le reste de l'intégrande (incluant dx). L'objectif est de rendre l'intégrale ∫ v du plus simple que ∫ u dv.
  • Comment gérer l'aire entre deux courbes si elles se croisent ?

    Diviser l'intervalle en sous-intervalles où soit f(x) ≥ g(x), soit g(x) ≥ f(x). Calculer l'intégrale sur chaque sous-intervalle séparément et prendre la valeur absolue des résultats avant de les additionner.