Mathématiques > Analyse > Continuité > Théorème des valeurs intermédiaires (TVI)

Théorème des Valeurs Intermédiaires (TVI)

Comprendre et appliquer le Théorème des Valeurs Intermédiaires (TVI) avec des exemples concrets et des exercices corrigés. Ce cours complet couvre les conditions d'application, les corollaires et les applications pratiques du TVI.

Introduction au TVI

Le Théorème des Valeurs Intermédiaires (TVI) est un théorème fondamental en analyse mathématique. Il permet de prouver l'existence de solutions pour certaines équations. En termes simples, il dit que si une fonction continue prend deux valeurs, alors elle prend toutes les valeurs intermédiaires entre ces deux valeurs. Ce théorème est particulièrement utile pour démontrer l'existence de racines d'une équation.

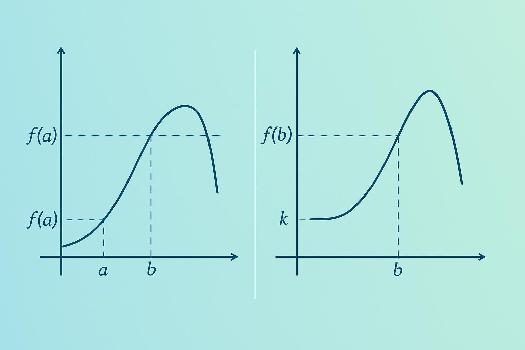
Énoncé du Théorème des Valeurs Intermédiaires

Soit f une fonction définie et continue sur un intervalle fermé [a, b]. Pour tout réel k compris entre f(a) et f(b) (c'est-à-dire f(a) ≤ k ≤ f(b) ou f(b) ≤ k ≤ f(a)), il existe au moins un réel c dans l'intervalle [a, b] tel que f(c) = k.

Conditions d'Application du TVI

Pour que le TVI puisse être appliqué, deux conditions essentielles doivent être remplies :

  1. Continuité de la fonction : La fonction f doit être continue sur l'intervalle [a, b]. La continuité signifie qu'il n'y a pas de 'sauts' ou de 'trous' dans le graphe de la fonction sur cet intervalle.
  2. Valeur intermédiaire : La valeur k doit être comprise entre f(a) et f(b). En d'autres termes, k doit se situer entre les valeurs que prend la fonction aux extrémités de l'intervalle.
Si l'une de ces conditions n'est pas vérifiée, le TVI ne peut pas être appliqué, et il n'est pas possible de conclure à l'existence d'une solution.

Corollaire du TVI : Existence d'une Racine

Un corollaire important du TVI est utilisé pour démontrer l'existence de racines d'une équation. Si f est une fonction continue sur [a, b] et si f(a) et f(b) sont de signes opposés (c'est-à-dire f(a) * f(b) < 0), alors il existe au moins un réel c dans l'intervalle [a, b] tel que f(c) = 0. Ce c est une racine de l'équation f(x) = 0. Exemple : Soit la fonction f(x) = x3 - 2x + 1 sur l'intervalle [0, 1].

  • f est une fonction polynomiale, donc elle est continue sur [0, 1].
  • f(0) = 1 et f(1) = 0.
Comme f(0) et f(1) sont de signes opposés, le corollaire du TVI nous permet de conclure qu'il existe au moins une racine de f(x) = 0 dans l'intervalle [0, 1].

Exemple d'Application du TVI

Considérons la fonction f(x) = x2 sur l'intervalle [0, 2]. Montrons qu'il existe un c dans [0, 2] tel que f(c) = 3/2.

  • f est continue sur [0, 2] car c'est un polynôme.
  • f(0) = 0 et f(2) = 4.
  • 3/2 est bien compris entre 0 et 4.
Donc, d'après le TVI, il existe un c dans [0, 2] tel que f(c) = 3/2. On peut trouver ce c en résolvant l'équation x2 = 3/2, ce qui donne x = √(3/2), qui appartient bien à [0, 2].

Utilisation de la stricte monotonie pour l'unicité de la solution

Si, en plus des conditions du TVI, la fonction f est strictement monotone (strictement croissante ou strictement décroissante) sur l'intervalle [a, b], alors la solution c telle que f(c) = k est unique. La stricte monotonie garantit qu'il ne peut y avoir qu'un seul point où la fonction prend la valeur k. Exemple : Soit la fonction f(x) = x3 + x sur l'intervalle [0, 1].

  • f est continue sur [0, 1] (car c'est un polynôme).
  • f(0) = 0 et f(1) = 2.
  • La valeur k = 1 est comprise entre 0 et 2.
  • La dérivée de f(x) est f'(x) = 3x2 + 1, qui est strictement positive sur [0, 1]. Donc f est strictement croissante sur cet intervalle.
Par conséquent, d'après le TVI et la stricte monotonie, il existe une unique solution c dans [0, 1] telle que f(c) = 1.

Limitations du TVI

Bien que puissant, le TVI a ses limites. Il garantit l'existence d'une solution, mais ne la donne pas explicitement. Il est possible qu'on ne puisse pas trouver la valeur exacte de *c* algébriquement, surtout pour des fonctions complexes. De plus, il nécessite la continuité de la fonction; s'il y a une discontinuité, le théorème ne s'applique pas. Par exemple, considérons une fonction qui passe d'une valeur négative à une valeur positive sans jamais être égale à zéro. Dans ce cas, la fonction est discontinue et le TVI ne peut pas être utilisé pour prouver l'existence d'une racine.

Ce qu'il faut retenir

  • Énoncé : Si f est continue sur [a, b], et k est entre f(a) et f(b), alors il existe au moins un c dans [a, b] tel que f(c) = k.
  • Conditions : Continuité de f sur [a, b] et k compris entre f(a) et f(b).
  • Corollaire : Si f(a) et f(b) ont des signes opposés, alors il existe au moins une racine de f(x) = 0 dans [a, b].
  • Monotonie : Si f est strictement monotone, la solution c est unique.
  • Limitations : Le TVI prouve l'existence mais ne donne pas la valeur exacte, et nécessite la continuité.

← Théorème Fondamental de l'Analyse : Un Guide Complet →

FAQ

  • Le TVI permet-il de trouver la valeur exacte de la solution ?

    Non, le TVI garantit seulement l'existence d'une solution. Il ne donne pas la valeur exacte, qui peut être difficile ou impossible à déterminer analytiquement.
  • Que se passe-t-il si la fonction n'est pas continue ?

    Si la fonction n'est pas continue sur l'intervalle considéré, le TVI ne peut pas être appliqué. L'existence d'une solution n'est alors pas garantie.
  • Peut-on utiliser le TVI pour montrer qu'une équation n'a pas de solution ?

    Non, le TVI sert à démontrer l'existence de solutions. Pour prouver qu'une équation n'a pas de solution, d'autres méthodes sont nécessaires.