Relation de congruence : Comprendre et maîtriser

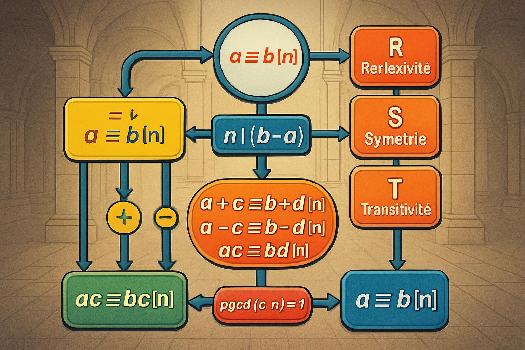
Définition de la congruence

La relation de congruence est une relation d'équivalence sur l'ensemble des entiers relatifs. Elle formalise l'idée de 'laisser le même reste dans une division euclidienne'.

Définition : Soient a, b, et n des entiers relatifs, avec n > 0. On dit que a est congru à b modulo n, et on note a ≡ b [n], si et seulement si n divise b - a. Autrement dit, b - a est un multiple de n. On peut aussi dire que a et b ont le même reste dans la division euclidienne par n.

Exemples

• Exemple 1 : 17 ≡ 2 [5] car 17 - 2 = 15, et 15 est divisible par 5. En effet, 17 divisé par 5 donne un quotient de 3 et un reste de 2. De même, 2 divisé par 5 donne un quotient de 0 et un reste de 2.
• Exemple 2 : 23 ≡ 3 [10] car 23 - 3 = 20, et 20 est divisible par 10. La division euclidienne de 23 par 10 donne un reste de 3.
• Exemple 3 : -5 ≡ 7 [4] car 7 - (-5) = 12, et 12 est divisible par 4.

Propriétés de la relation de congruence

La relation de congruence possède plusieurs propriétés importantes qui facilitent les calculs et les démonstrations. Voici les principales:

• Réflexivité : Pour tout entier a, a ≡ a [n]. En effet, a - a = 0, et 0 est divisible par n.
• Symétrie : Si a ≡ b [n], alors b ≡ a [n]. En effet, si n divise b - a, alors n divise aussi a - b = -(b - a).
• Transitivité : Si a ≡ b [n] et b ≡ c [n], alors a ≡ c [n]. En effet, si n divise b - a et n divise c - b, alors n divise aussi (b - a) + (c - b) = c - a.

Opérations compatibles avec la congruence

La relation de congruence est compatible avec les opérations d'addition, de soustraction et de multiplication.

1. Addition et Soustraction : Si a ≡ b [n] et c ≡ d [n], alors a + c ≡ b + d [n] et a - c ≡ b - d [n].

2. Multiplication : Si a ≡ b [n] et c ≡ d [n], alors ac ≡ bd [n].

3. Multiplication par un entier : Si a ≡ b [n], alors pour tout entier k, ka ≡ kb [n].

Conséquence importante : Si a ≡ b [n], alors pour tout entier naturel k, a^k ≡ b^k [n]. Cette propriété est cruciale pour simplifier les calculs de puissances modulo n.

Simplification des congruences

Il est parfois possible de simplifier une congruence en divisant les deux membres et le module par un diviseur commun.

Théorème : Si ac ≡ bc [n] et si c est premier avec n (c'est-à-dire que pgcd(c, n) = 1), alors a ≡ b [n].

Attention : Si pgcd(c, n) ≠ 1, on ne peut pas simplifier directement. Dans ce cas, on peut simplifier en divisant a, b, et n par leur pgcd avec c. Par exemple, si ac ≡ bc [nc], alors a ≡ b [n].

Applications de la congruence

La relation de congruence a de nombreuses applications en arithmétique, notamment :

• Tests de divisibilité : La congruence permet d'établir des tests de divisibilité rapides. Par exemple, un nombre est divisible par 3 si et seulement si la somme de ses chiffres est divisible par 3. Cela découle de la congruence 10 ≡ 1 [3].
• Résolution d'équations diophantiennes linéaires : La congruence est un outil essentiel pour déterminer si une équation diophantienne linéaire (de la forme ax + by = c, où a, b, c sont des entiers) a des solutions, et pour trouver ces solutions.
• Cryptographie : La congruence est à la base de nombreux algorithmes de cryptographie moderne, notamment le chiffrement RSA.
• Calcul de restes : La congruence permet de calculer rapidement le reste d'une division euclidienne, même pour des nombres très grands.

Ce qu'il faut retenir

• Définition : a ≡ b [n] si et seulement si n divise b - a.
• Propriétés : Réflexivité, symétrie, transitivité.
• Compatibilité : Addition, soustraction, multiplication. Si a ≡ b [n] et c ≡ d [n], alors a + c ≡ b + d [n], a - c ≡ b - d [n], et ac ≡ bd [n].
• Simplification : Si ac ≡ bc [n] et pgcd(c, n) = 1, alors a ≡ b [n].
• Applications : Tests de divisibilité, équations diophantiennes, cryptographie, calcul de restes.