Mathématiques > Graphes (Terminale - Spécialité) > Introduction aux Graphes > Représentation des graphes (matrice d'adjacence, liste d'adjacence)

Représentation des Graphes : Matrices et Listes d'Adjacence

Découvrez les méthodes de représentation des graphes : matrices d'adjacence et listes d'adjacence. Comprenez leurs avantages et inconvénients pour résoudre des problèmes concrets.

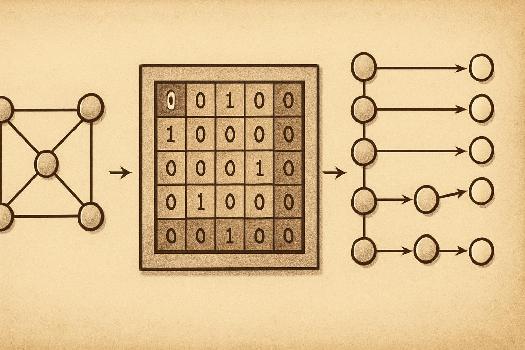
Introduction : Pourquoi Représenter un Graphe ?

La représentation d'un graphe est fondamentale pour pouvoir manipuler et analyser ses propriétés avec des outils informatiques. Un graphe, qui est une structure composée de nœuds (sommets) reliés par des arêtes, peut modéliser une grande variété de situations : réseaux sociaux, réseaux routiers, relations entre personnes, etc. Pour pouvoir appliquer des algorithmes (par exemple, trouver le plus court chemin), il faut d'abord traduire le graphe dans un format compréhensible par un ordinateur. Deux méthodes principales existent : la matrice d'adjacence et la liste d'adjacence.

La Matrice d'Adjacence

Une matrice d'adjacence est un tableau carré où les lignes et les colonnes représentent les sommets du graphe. La valeur à l'intersection de la ligne *i* et de la colonne *j* indique s'il existe une arête reliant le sommet *i* au sommet *j*. Construction :

  • On crée une matrice carrée de taille *n x n*, où *n* est le nombre de sommets dans le graphe.
  • Si une arête relie le sommet *i* au sommet *j*, on met la valeur 1 à la position (i, j) de la matrice. Sinon, on met 0.
  • Dans le cas d'un graphe non orienté, si une arête relie *i* à *j*, alors on met 1 à la fois en (i, j) et en (j, i) car la relation est bidirectionnelle.
  • Dans le cas d'un graphe orienté, la présence d'un 1 en (i, j) indique seulement une arête allant de *i* vers *j*, pas nécessairement l'inverse.
Exemple : Considérons un graphe avec 4 sommets (A, B, C, D) et les arêtes suivantes : A-B, A-C, B-C, C-D. La matrice d'adjacence correspondante serait:
ABCD
A0110
B1010
C1101
D0010
Avantages :
  • Simple à implémenter et à comprendre.
  • Vérifier rapidement si une arête existe entre deux sommets (accès direct en O(1)).
Inconvénients :
  • Requiert beaucoup d'espace mémoire, surtout pour les graphes creux (ceux qui ont peu d'arêtes). La complexité spatiale est de O(n²).
  • Peu efficace pour itérer sur les voisins d'un sommet, car il faut parcourir toute une ligne de la matrice.

La Liste d'Adjacence

Une liste d'adjacence représente un graphe en associant à chaque sommet une liste de ses voisins. Autrement dit, pour chaque sommet, on enregistre tous les sommets auxquels il est directement connecté. Construction :

  • On crée un tableau (ou dictionnaire) de *n* éléments, où *n* est le nombre de sommets.
  • Chaque élément du tableau représente un sommet du graphe.
  • Pour chaque sommet, on stocke une liste de ses voisins (les sommets auxquels il est relié par une arête).
  • Dans le cas d'un graphe non orienté, si *j* est un voisin de *i*, alors *i* est aussi un voisin de *j*.
  • Dans le cas d'un graphe orienté, on indique seulement les sommets vers lesquels partent les arêtes.
Exemple : Reprenons le même graphe que précédemment (4 sommets : A, B, C, D, et arêtes : A-B, A-C, B-C, C-D). La liste d'adjacence correspondante serait:
  • A : [B, C]
  • B : [A, C]
  • C : [A, B, D]
  • D : [C]
Avantages :
  • Plus économe en mémoire que la matrice d'adjacence pour les graphes creux. La complexité spatiale est de O(n + m), où *n* est le nombre de sommets et *m* le nombre d'arêtes.
  • Efficace pour itérer sur les voisins d'un sommet.
Inconvénients :
  • Vérifier si une arête existe entre deux sommets est plus lent qu'avec une matrice d'adjacence (il faut parcourir la liste des voisins).
  • L'implémentation peut être un peu plus complexe que celle de la matrice d'adjacence.

Choix de la Représentation

Le choix entre la matrice d'adjacence et la liste d'adjacence dépend du type de graphe et des opérations que l'on souhaite effectuer le plus fréquemment.

  • Si le graphe est dense (beaucoup d'arêtes) et que l'on a besoin de vérifier rapidement l'existence d'une arête, la matrice d'adjacence est souvent préférable.
  • Si le graphe est creux (peu d'arêtes) et que l'on doit souvent itérer sur les voisins d'un sommet, la liste d'adjacence est plus adaptée.
En pratique, la liste d'adjacence est souvent privilégiée pour les graphes de grande taille, car elle est plus économe en mémoire.

Ce qu'il faut retenir

  • Matrice d'adjacence : Tableau carré qui indique la présence ou l'absence d'arêtes entre les sommets. Facile à implémenter, rapide pour vérifier l'existence d'une arête, mais consomme beaucoup de mémoire pour les graphes creux.
  • Liste d'adjacence : Associe à chaque sommet la liste de ses voisins. Plus économe en mémoire pour les graphes creux, efficace pour itérer sur les voisins, mais plus lente pour vérifier l'existence d'une arête.
  • Le choix entre les deux représentations dépend de la densité du graphe et des opérations à effectuer.

← L'Algorithme de Dijkstra : Trouver le Plus Court Chemin →

FAQ

  • Quelle est la complexité spatiale de la matrice d'adjacence ?

    La complexité spatiale de la matrice d'adjacence est de O(n²), où n est le nombre de sommets du graphe. Cela signifie que l'espace mémoire nécessaire croît quadratiquement avec le nombre de sommets.
  • Quelle est la complexité spatiale de la liste d'adjacence ?

    La complexité spatiale de la liste d'adjacence est de O(n + m), où n est le nombre de sommets et m le nombre d'arêtes du graphe. Pour les graphes creux (m est petit par rapport à n²), la liste d'adjacence est plus économe en mémoire que la matrice d'adjacence.
  • Comment représenter un graphe pondéré (avec des poids sur les arêtes) avec une matrice d'adjacence ?

    Dans une matrice d'adjacence pour un graphe pondéré, au lieu de mettre 1 pour indiquer la présence d'une arête, on met le poids de l'arête. Si il n'y a pas d'arête on met 0 ou infini suivant l'application.