Forme Exponentielle d'un Nombre Complexe

Introduction à la Forme Exponentielle

La forme exponentielle d'un nombre complexe est une manière concise et élégante de représenter ce nombre. Elle est particulièrement utile pour effectuer des opérations telles que la multiplication, la division, et l'élévation à une puissance. Pour comprendre la forme exponentielle, nous devons d'abord comprendre les formes algébrique et trigonométrique des nombres complexes.

Rappel : Forme Algébrique et Trigonométrique

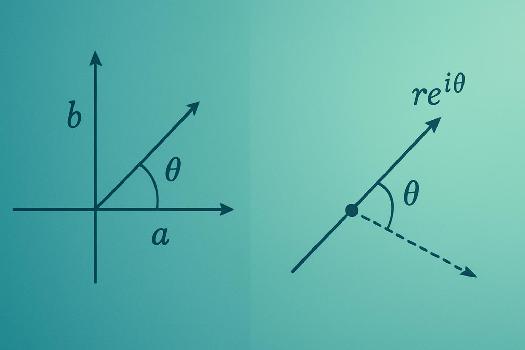
Un nombre complexe *z* peut être écrit sous sa forme algébrique : z = a + ib, où a est la partie réelle (Re(z)) et b est la partie imaginaire (Im(z)), et i est l'unité imaginaire (i² = -1). Un même nombre complexe *z* peut aussi être écrit sous sa forme trigonométrique : z = r(cos θ + i sin θ), où *r* est le module de *z* (r = |z|) et θ est un argument de *z* (θ = arg(z)).

Définition de la Forme Exponentielle

La forme exponentielle d'un nombre complexe *z* est donnée par : z = re^iθ, où *r* est le module de *z* et θ est un argument de *z*, et e est la base du logarithme népérien (e ≈ 2.71828). La relation fondamentale qui relie la forme exponentielle à la forme trigonométrique est la formule d'Euler : e^iθ = cos θ + i sin θ. En utilisant la formule d'Euler, nous pouvons facilement passer de la forme exponentielle à la forme trigonométrique et vice versa.

Passage de la Forme Algébrique à la Forme Exponentielle

Pour passer de la forme algébrique z = a + ib à la forme exponentielle z = re^iθ, nous devons déterminer le module *r* et un argument θ de *z*. Calcul du module : r = |z| = √(a² + b²). Calcul de l'argument : θ est tel que cos θ = a/r et sin θ = b/r. La détermination précise de θ nécessite une attention particulière au quadrant dans lequel se trouve le point (a, b) dans le plan complexe. Utiliser la fonction arctangente (tan^-1 ou atan) peut être utile, mais il faut ajuster l'angle en fonction du signe de *a* et *b* pour obtenir la bonne valeur de θ dans l'intervalle approprié (par exemple, (-π, π]). Une fois *r* et θ déterminés, on peut écrire le nombre complexe sous sa forme exponentielle : z = re^iθ.

Exemples

Exemple 1: Soit z = 1 + i. Calcul du module : r = √(1² + 1²) = √2. Calcul de l'argument : cos θ = 1/√2 et sin θ = 1/√2, donc θ = π/4. Forme exponentielle : z = √2e^iπ/4. Exemple 2: Soit z = -2i. Calcul du module : r = √((-2)²)= 2. Calcul de l'argument : cos θ = 0 et sin θ = -1, donc θ = -π/2. Forme exponentielle : z = 2e^-iπ/2. Exemple 3: Soit z = -1 + i√3. Calcul du module : r = √((-1)² + (√3)²) = √(1+3) = 2. Calcul de l'argument : cos θ = -1/2 et sin θ = √3/2, donc θ = 2π/3. Forme exponentielle : z = 2e^i2π/3.

Opérations avec la Forme Exponentielle

La forme exponentielle simplifie considérablement les opérations sur les nombres complexes : Multiplication: Si z₁ = r₁e^iθ₁ et z₂ = r₂e^iθ₂, alors z₁z₂ = r₁r₂e^{i(θ₁+θ₂)}. Le module est le produit des modules et l'argument est la somme des arguments. Division: Si z₁ = r₁e^iθ₁ et z₂ = r₂e^iθ₂ (avec z₂ ≠ 0), alors z₁/z₂ = (r₁/r₂)e^{i(θ₁-θ₂)}. Le module est le quotient des modules et l'argument est la différence des arguments. Puissance: Si z = re^iθ, alors zⁿ = rⁿe^inθ pour tout entier n. Cette formule est connue sous le nom de formule de De Moivre. Conjugué: Si z = re^iθ, alors le conjugué de z est z̄ = re^-iθ.

Applications

La forme exponentielle est utilisée dans de nombreux domaines des mathématiques et de la physique, notamment : Résolution d'équations: Elle simplifie la résolution d'équations complexes, en particulier celles impliquant des puissances. Analyse de circuits électriques: Elle est utilisée pour représenter les impédances et les tensions alternatives. Mécanique quantique: Elle est utilisée pour décrire les fonctions d'onde. Traitement du signal: Elle est utilisée dans l'analyse de Fourier et le traitement des signaux périodiques.

Ce qu'il faut retenir

• Forme exponentielle: z = re^iθ, où r est le module et θ un argument.
• Formule d'Euler: e^iθ = cos θ + i sin θ.
• Passage algébrique à exponentielle: Calculer r = √(a² + b²) et trouver θ tel que cos θ = a/r et sin θ = b/r.
• Multiplication: Les modules se multiplient, les arguments s'additionnent.
• Division: Les modules se divisent, les arguments se soustraient.
• Puissance (De Moivre): (re^iθ)ⁿ = rⁿe^inθ.
• Conjugué: z̄ = re^-iθ.