Mathématiques > Algèbre > Équations et Inéquations > Inéquations avec valeurs absolues

Inéquations avec Valeurs Absolues : Guide Complet pour le Lycée

Apprenez à résoudre les inéquations avec valeurs absolues grâce à ce guide détaillé, conçu pour les élèves de lycée. Comprenez les principes fondamentaux, les différentes méthodes de résolution, et entraînez-vous avec des exemples variés et progressifs.

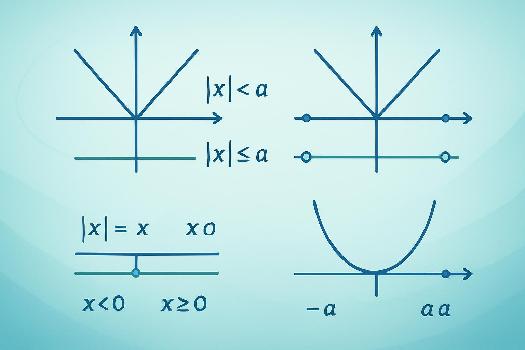
Introduction à la Valeur Absolue

La valeur absolue d'un nombre réel x, notée |x|, est sa distance à zéro sur la droite numérique. Elle est toujours non négative. Formellement:

  • Si x ≥ 0, alors |x| = x.
  • Si x < 0, alors |x| = -x.
Par exemple, |3| = 3 et |-3| = 3. Cette définition est cruciale pour comprendre comment résoudre les inéquations impliquant des valeurs absolues.

Principe de Résolution des Inéquations avec Valeurs Absolues

Résoudre une inéquation avec une valeur absolue revient à considérer deux cas distincts, en raison de la définition de la valeur absolue :

  • Cas 1 : L'expression à l'intérieur de la valeur absolue est positive ou nulle.
  • Cas 2 : L'expression à l'intérieur de la valeur absolue est négative.
Nous allons explorer comment appliquer ce principe à différents types d'inéquations.

Inéquations de la Forme |x| < a (où a > 0)

L'inéquation |x| < a (avec a > 0) signifie que la distance de x à zéro est inférieure à a. Cela équivaut à dire que x est compris entre -a et a. Traduction en double inégalité: |x| < a ⇔ -a < x < a Exemple: Résolvons |x| < 5. La solution est l'ensemble des nombres x tels que -5 < x < 5. En notation d'intervalle, la solution est ]-5, 5[.

Inéquations de la Forme |x| ≤ a (où a > 0)

L'inéquation |x| ≤ a (avec a > 0) signifie que la distance de x à zéro est inférieure ou égale à a. Cela inclut les bornes -a et a. Traduction en double inégalité: |x| ≤ a ⇔ -a ≤ x ≤ a Exemple: Résolvons |x| ≤ 2. La solution est l'ensemble des nombres x tels que -2 ≤ x ≤ 2. En notation d'intervalle, la solution est [-2, 2].

Inéquations de la Forme |x| > a (où a > 0)

L'inéquation |x| > a (avec a > 0) signifie que la distance de x à zéro est supérieure à a. Cela équivaut à dire que x est soit inférieur à -a, soit supérieur à a. Traduction en union d'inégalités: |x| > a ⇔ x < -a ou x > a Exemple: Résolvons |x| > 3. La solution est l'ensemble des nombres x tels que x < -3 ou x > 3. En notation d'intervalle, la solution est ]-∞, -3[ ∪ ]3, +∞[.

Inéquations de la Forme |x| ≥ a (où a > 0)

L'inéquation |x| ≥ a (avec a > 0) signifie que la distance de x à zéro est supérieure ou égale à a. Cela inclut les bornes -a et a. Traduction en union d'inégalités: |x| ≥ a ⇔ x ≤ -a ou x ≥ a Exemple: Résolvons |x| ≥ 1. La solution est l'ensemble des nombres x tels que x ≤ -1 ou x ≥ 1. En notation d'intervalle, la solution est ]-∞, -1] ∪ [1, +∞[.

Inéquations avec des Expressions Algébriques plus Complexes

Les principes restent les mêmes lorsque l'intérieur de la valeur absolue est une expression plus complexe. Il faut toujours considérer les deux cas:

  • Cas 1: L'expression à l'intérieur de la valeur absolue est positive ou nulle.
  • Cas 2: L'expression à l'intérieur de la valeur absolue est négative.
Exemple: Résolvons |2x - 1| < 3.
  • Cas 1: 2x - 1 ≥ 0 (donc x ≥ 1/2). Alors |2x - 1| = 2x - 1. L'inéquation devient 2x - 1 < 3, ce qui donne 2x < 4, donc x < 2. La solution dans ce cas est 1/2 ≤ x < 2.
  • Cas 2: 2x - 1 < 0 (donc x < 1/2). Alors |2x - 1| = -(2x - 1) = -2x + 1. L'inéquation devient -2x + 1 < 3, ce qui donne -2x < 2, donc x > -1. La solution dans ce cas est -1 < x < 1/2.
La solution globale est l'union des solutions des deux cas: ]-1, 2[.

Méthode Alternative : Utilisation des Carrés

Parfois, pour simplifier la résolution d'inéquations avec valeurs absolues, il peut être utile d'élever les deux côtés au carré. Cependant, cette méthode doit être utilisée avec précaution. Règle: Si a et b sont des nombres réels non négatifs, alors a < b si et seulement si a2 < b2. Exemple: Résolvons |x + 1| > 2. En élevant les deux côtés au carré, on obtient (x + 1)2 > 4, ce qui se développe en x2 + 2x + 1 > 4, soit x2 + 2x - 3 > 0. On factorise le trinôme: (x + 3)(x - 1) > 0. L'étude du signe de ce produit donne les solutions x < -3 ou x > 1. En notation d'intervalle, la solution est ]-∞, -3[ ∪ ]1, +∞[. Attention: Cette méthode ne fonctionne que si les deux côtés de l'inéquation sont non négatifs. Il faut s'assurer de cela avant d'élever au carré.

Ce qu'il faut retenir

  • Définition de la valeur absolue: |x| = x si x ≥ 0 et |x| = -x si x < 0.
  • |x| < a (a > 0): ⇔ -a < x < a.
  • |x| ≤ a (a > 0): ⇔ -a ≤ x ≤ a.
  • |x| > a (a > 0): ⇔ x < -a ou x > a.
  • |x| ≥ a (a > 0): ⇔ x ≤ -a ou x ≥ a.
  • Résolution générale: Considérer les cas où l'expression à l'intérieur de la valeur absolue est positive/nulle et négative.
  • Méthode des carrés: Peut être utilisée si les deux côtés de l'inéquation sont non négatifs.

← Introduction à la Représentation Graphique des Fonctions Inéquations du premier degré : Guide de résolution →

FAQ

  • Comment savoir si je dois utiliser la méthode des carrés ?

    La méthode des carrés est utile lorsque vous avez une inéquation avec des valeurs absolues des deux côtés, ou lorsque vous voulez vous débarrasser de la valeur absolue pour simplifier l'équation. Assurez-vous que les deux côtés de l'inéquation sont non négatifs avant d'élever au carré.
  • Que faire si l'inéquation est de la forme |f(x)| < g(x), où g(x) peut être négatif ?

    Il faut d'abord s'assurer que g(x) est positif. Si g(x) est négatif, l'inéquation n'a pas de solution. Si g(x) est positif, on peut alors résoudre en considérant les deux cas comme d'habitude : f(x) < g(x) et -f(x) < g(x).