Exercices Corrigés: Maîtriser le Cercle Trigonométrique

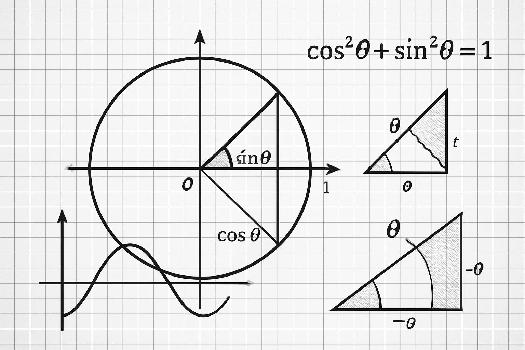
Exercice 1: Calcul de sinus et cosinus

Énoncé: Sachant que sin(π/6) = 1/2, déterminez cos(π/6) en utilisant le cercle trigonométrique.

Solution:

1. On sait que cos²(θ) + sin²(θ) = 1.
2. Donc cos²(π/6) + (1/2)² = 1.
3. cos²(π/6) = 1 - 1/4 = 3/4.
4. cos(π/6) = ±√(3/4) = ±√3/2.
5. Puisque π/6 est dans le premier quadrant, cos(π/6) est positif. Donc cos(π/6) = √3/2.

Exercice 2: Résolution d'équation trigonométrique

Énoncé: Résolvez l'équation sin(x) = -√2/2 dans l'intervalle [0, 2π[.

Solution:

1. On cherche les angles x dont le sinus est -√2/2.
2. On sait que sin(5π/4) = -√2/2 et sin(7π/4) = -√2/2.
3. Donc les solutions dans l'intervalle [0, 2π[ sont x = 5π/4 et x = 7π/4.

Exercice 3: Utilisation des angles associés

Énoncé: Exprimez cos(2π/3) en fonction de cos(π/3).

Solution:

1. On peut écrire 2π/3 = π - π/3.
2. On utilise la relation cos(π - θ) = -cos(θ).
3. Donc cos(2π/3) = cos(π - π/3) = -cos(π/3).
4. Puisque cos(π/3) = 1/2, on a cos(2π/3) = -1/2.

Exercice 4: Calcul de tangente

Énoncé: Sachant que sin(π/4)=√2/2 et cos(π/4)=√2/2, calculez tan(π/4).

Solution:

1. On utilise la relation tan(θ) = sin(θ)/cos(θ)
2. Donc tan(π/4) = (√2/2) / (√2/2) = 1

Ce qu'il faut retenir

• La relation fondamentale cos²(θ) + sin²(θ) = 1 est essentielle pour calculer les sinus et cosinus.
• Le cercle trigonométrique permet de visualiser les solutions des équations trigonométriques.
• Connaître les relations entre les angles associés facilite les calculs.
• L'utilisation du cercle trigonométrique permet de comprendre et de résoudre de nombreux problèmes de trigonométrie.