Mathématiques > Nombres Complexes (Terminale) > Applications Géométriques > Interprétation géométrique des nombres complexes (affixe, point image)

Interprétation Géométrique des Nombres Complexes : Affixe et Point Image

Explorez l'interprétation géométrique des nombres complexes, en comprenant comment associer un nombre complexe à un point du plan complexe et vice versa. Découvrez le concept d'affixe et son rôle essentiel dans la représentation géométrique des nombres complexes.

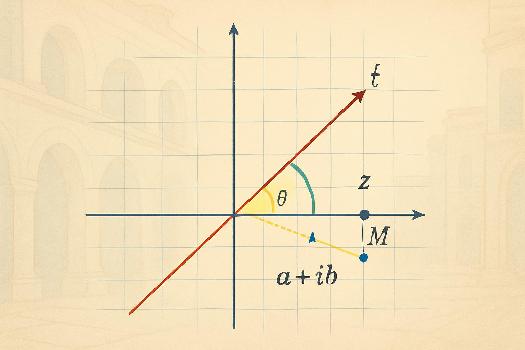
Introduction au Plan Complexe

Le plan complexe, aussi appelé plan d'Argand, est un plan où l'axe des abscisses représente la partie réelle d'un nombre complexe et l'axe des ordonnées représente sa partie imaginaire. Chaque point du plan correspond ainsi à un nombre complexe unique, et inversement. Comprendre cette représentation est crucial pour l'interprétation géométrique des nombres complexes.

Définition de l'Affixe

L'affixe d'un point M dans le plan complexe est le nombre complexe z = a + ib qui lui est associé, où 'a' est l'abscisse de M et 'b' est son ordonnée. On note souvent z = aff(M). Ainsi, chaque point du plan complexe a une affixe unique, et chaque nombre complexe correspond à un point unique dans le plan. Visualisez cela comme un système de coordonnées où les nombres complexes sont les 'coordonnées' des points.

Point Image d'un Nombre Complexe

Le point image d'un nombre complexe z = a + ib est le point M du plan complexe dont les coordonnées sont (a, b). En d'autres termes, M est le point dont l'affixe est z. La correspondance entre un nombre complexe et son point image est fondamentale pour traduire des propriétés algébriques des nombres complexes en propriétés géométriques des points du plan. Par exemple, si z = 2 + 3i, alors le point image de z est le point M de coordonnées (2, 3).

Représentation Graphique

Pour représenter graphiquement un nombre complexe, on trace un vecteur partant de l'origine du plan complexe jusqu'au point image du nombre complexe. La longueur de ce vecteur représente le module du nombre complexe, et l'angle que ce vecteur forme avec l'axe des abscisses représente l'argument du nombre complexe. Cette représentation vectorielle permet de visualiser les opérations sur les nombres complexes, comme l'addition et la multiplication.

Exemples Concrets

  • Exemple 1: Soit z = 1 + i. Son point image est le point M de coordonnées (1, 1).
  • Exemple 2: Soit z = -2 - i. Son point image est le point N de coordonnées (-2, -1).
  • Exemple 3: Soit le point P de coordonnées (0, 3). Son affixe est z = 3i.
Ces exemples illustrent la relation directe entre les nombres complexes et leurs représentations géométriques dans le plan complexe.

Applications

L'interprétation géométrique des nombres complexes est utilisée dans de nombreux domaines, notamment :

  • Géométrie: Démonstration de propriétés géométriques (alignement de points, cocyclicité, etc.)
  • Physique: Représentation de phénomènes ondulatoires, mécanique quantique.
  • Informatique: Traitement du signal, infographie.
Comprendre cette interprétation permet de résoudre des problèmes complexes de manière élégante et intuitive.

Ce qu'il faut retenir

  • Plan Complexe : Un plan où l'axe des abscisses représente la partie réelle et l'axe des ordonnées la partie imaginaire d'un nombre complexe.
  • Affixe : Le nombre complexe associé à un point du plan complexe. Si M a pour coordonnées (a, b), alors aff(M) = a + ib.
  • Point Image : Le point du plan complexe associé à un nombre complexe. Si z = a + ib, alors son point image est M(a, b).
  • Représentation Graphique : Un nombre complexe peut être représenté par un vecteur partant de l'origine jusqu'à son point image. La longueur du vecteur est le module, et l'angle avec l'axe des abscisses est l'argument.

← Formule de Moivre : Introduction et Applications Introduction aux Nombres Complexes: Définition et Forme Algébrique →

FAQ

  • Quelle est la différence entre un nombre complexe et son affixe ?

    Un nombre complexe est une entité algébrique de la forme a + ib. L'affixe est simplement le terme que l'on utilise pour désigner ce nombre complexe lorsqu'il est associé à un point du plan complexe.
  • Comment trouver l'affixe du milieu d'un segment [AB] ?

    L'affixe du milieu du segment [AB] est la moyenne des affixes de A et B. Si aff(A) = z_A et aff(B) = z_B, alors l'affixe du milieu est (z_A + z_B) / 2.
  • Pourquoi utilise-t-on les nombres complexes en géométrie ?

    Les nombres complexes permettent de traduire des propriétés géométriques en relations algébriques, ce qui simplifie souvent les démonstrations et les calculs. Ils offrent une approche élégante et puissante pour résoudre des problèmes de géométrie.