Mathématiques > Nombres Complexes (Terminale) > Introduction aux Nombres Complexes > Opérations sur les nombres complexes (addition, soustraction, multiplication)

Opérations sur les Nombres Complexes

Explorez l'addition, la soustraction et la multiplication des nombres complexes. Apprenez les règles et les techniques pour maîtriser ces opérations essentielles.

Définition d'un Nombre Complexe

Un nombre complexe est un nombre de la forme z = a + bi, où a et b sont des nombres réels, et i est l'unité imaginaire, définie par i2 = -1. Le nombre a est appelé la partie réelle de z, notée Re(z), et b est appelé la partie imaginaire de z, notée Im(z).

Addition des Nombres Complexes

Pour additionner deux nombres complexes, on additionne leurs parties réelles et leurs parties imaginaires séparément.

Soient z1 = a + bi et z2 = c + di deux nombres complexes. Alors, leur somme est donnée par :

z1 + z2 = (a + c) + (b + d)i

Exemple :
Si z1 = 3 + 2i et z2 = 1 - 4i, alors:
z1 + z2 = (3 + 1) + (2 - 4)i = 4 - 2i

Soustraction des Nombres Complexes

Pour soustraire deux nombres complexes, on soustrait leurs parties réelles et leurs parties imaginaires séparément.

Soient z1 = a + bi et z2 = c + di deux nombres complexes. Alors, leur différence est donnée par :

z1 - z2 = (a - c) + (b - d)i

Exemple :
Si z1 = 5 - i et z2 = 2 + 3i, alors:
z1 - z2 = (5 - 2) + (-1 - 3)i = 3 - 4i

Multiplication des Nombres Complexes

Pour multiplier deux nombres complexes, on utilise la distributivité et la propriété i2 = -1.

Soient z1 = a + bi et z2 = c + di deux nombres complexes. Alors, leur produit est donné par :

z1 * z2 = (a + bi)(c + di) = ac + adi + bci + bdi2 = ac + adi + bci - bd = (ac - bd) + (ad + bc)i

Exemple :
Si z1 = 2 + i et z2 = 3 - 2i, alors:
z1 * z2 = (2 + i)(3 - 2i) = 2*3 + 2*(-2i) + i*3 + i*(-2i) = 6 - 4i + 3i - 2i2 = 6 - i - 2(-1) = 6 - i + 2 = 8 - i

Exemples Combinés

Prenons trois nombres complexes: z1 = 1 + i, z2 = 2 - i, et z3 = -1 + 2i.

Calculons z1 + z2 * z3:

D'abord, on calcule z2 * z3:
z2 * z3 = (2 - i)(-1 + 2i) = 2*(-1) + 2*(2i) - i*(-1) - i*(2i) = -2 + 4i + i - 2i2 = -2 + 5i - 2(-1) = -2 + 5i + 2 = 5i

Ensuite, on additionne z1 au résultat:
z1 + z2 * z3 = (1 + i) + 5i = 1 + 6i

Ce qu'il faut retenir

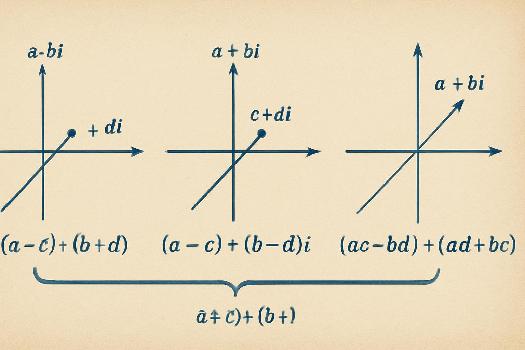
  • Addition : Additionner les parties réelles entre elles et les parties imaginaires entre elles : (a + bi) + (c + di) = (a + c) + (b + d)i.
  • Soustraction : Soustraire les parties réelles entre elles et les parties imaginaires entre elles : (a + bi) - (c + di) = (a - c) + (b - d)i.
  • Multiplication : Utiliser la distributivité et la propriété i2 = -1 : (a + bi)(c + di) = (ac - bd) + (ad + bc)i.
Il est crucial de simplifier l'expression après chaque opération pour obtenir le résultat sous la forme a + bi.

← Introduction aux Nombres Complexes: Définition et Forme Algébrique Résolution d'Équations Complexes et Interprétation Géométrique →

FAQ

  • Comment simplifier une expression complexe après une multiplication ?

    Après avoir appliqué la distributivité lors de la multiplication, remplacez chaque i2 par -1. Ensuite, regroupez les termes réels et les termes imaginaires pour obtenir le résultat final sous la forme a + bi.
  • Pourquoi est-il important de connaître ces opérations ?

    Les opérations sur les nombres complexes sont fondamentales en mathématiques et en physique. Elles sont utilisées dans de nombreux domaines, tels que l'électronique, la mécanique quantique et le traitement du signal. Une bonne compréhension de ces opérations facilite la résolution de problèmes complexes dans ces domaines.