Vecteurs dans l'espace : Coordonnées et Opérations

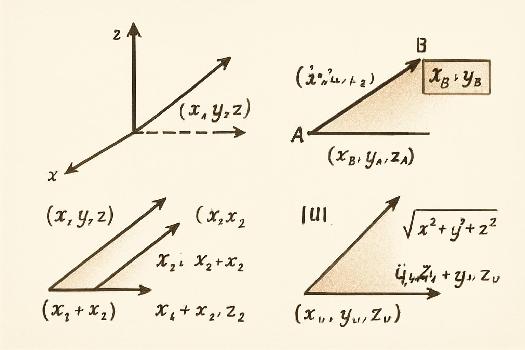
Introduction aux vecteurs dans l'espace

Un vecteur dans l'espace est une entité mathématique définie par une direction, un sens et une longueur (ou norme). Contrairement à un point, un vecteur ne possède pas de position fixe dans l'espace. On peut le translater sans le modifier. Les vecteurs sont essentiels pour décrire des translations, des forces, des vitesses, etc. Dans un repère cartésien (O, i, j, k), on peut représenter un vecteur par ses coordonnées.

Coordonnées d'un vecteur

Soit un vecteur u. Ses coordonnées (x, y, z) dans le repère (O, i, j, k) sont définies de la manière suivante :

u = xi + yj + zk

x est la composante de u selon l'axe x.

y est la composante de u selon l'axe y.

z est la composante de u selon l'axe z.

On note souvent u(x, y, z). Ces coordonnées représentent les déplacements dans les directions des axes pour aller du point initial au point final du vecteur.

Calcul des coordonnées d'un vecteur à partir de deux points

Soient deux points A(x_A, y_A, z_A) et B(x_B, y_B, z_B) dans l'espace. Le vecteur AB a pour coordonnées :

AB(x_B - x_A, y_B - y_A, z_B - z_A)

C'est-à-dire qu'on soustrait les coordonnées du point initial (A) aux coordonnées du point final (B).

Opérations sur les vecteurs

Comme pour les vecteurs du plan, on peut effectuer plusieurs opérations sur les vecteurs dans l'espace :

Addition : Soient u(x_u, y_u, z_u) et v(x_v, y_v, z_v). Alors, u + v = (x_u + x_v, y_u + y_v, z_u + z_v). On additionne les composantes correspondantes.

Soustraction : Soient u(x_u, y_u, z_u) et v(x_v, y_v, z_v). Alors, u - v = (x_u - x_v, y_u - y_v, z_u - z_v). On soustrait les composantes correspondantes.

Multiplication par un scalaire : Soit u(x, y, z) et un scalaire k (un nombre réel). Alors, ku = (kx, ky, kz). On multiplie chaque composante par le scalaire.

Norme d'un vecteur

La norme (ou longueur) d'un vecteur u(x, y, z), notée ||u||, est donnée par :

||u|| = √(x² + y² + z²)

Cette formule est une extension du théorème de Pythagore en trois dimensions.

Vecteurs colinéaires

Deux vecteurs u et v sont colinéaires s'il existe un scalaire k tel que u = kv. Autrement dit, leurs coordonnées sont proportionnelles. Cela signifie qu'ils ont la même direction ou des directions opposées.

Produit scalaire de deux vecteurs

Le produit scalaire de deux vecteurs u(x_u, y_u, z_u) et v(x_v, y_v, z_v), noté u.v, est donné par :

u.v = x_ux_v + y_uy_v + z_uz_v

Une autre formule pour calculer le produit scalaire est : u.v = ||u|| ||v|| cos(θ), où θ est l'angle entre les vecteurs u et v. Si u.v = 0, alors les vecteurs u et v sont orthogonaux (perpendiculaires).

Applications des vecteurs dans l'espace

Les vecteurs dans l'espace sont utilisés dans de nombreux domaines :

• Physique : Pour représenter des forces, des vitesses, des accélérations.
• Infographie : Pour les transformations géométriques (translations, rotations, mises à l'échelle) d'objets 3D.
• Navigation : Pour calculer des trajectoires et des distances.
• Jeux vidéo : Pour le mouvement des personnages et des objets, ainsi que pour la gestion de la physique du jeu.

Ce qu'il faut retenir

• Un vecteur dans l'espace est défini par ses coordonnées (x, y, z) dans un repère cartésien.
• Les coordonnées du vecteur AB sont (x_B - x_A, y_B - y_A, z_B - z_A).
• Les opérations sur les vecteurs (addition, soustraction, multiplication par un scalaire) se font composante par composante.
• La norme d'un vecteur u(x, y, z) est ||u|| = √(x² + y² + z²).
• Le produit scalaire de deux vecteurs u(x_u, y_u, z_u) et v(x_v, y_v, z_v) est u.v = x_ux_v + y_uy_v + z_uz_v.
• Deux vecteurs sont orthogonaux si leur produit scalaire est nul.