Mathématiques > Géométrie > Géométrie Plane > Théorème de Thalès et sa réciproque

Le Théorème de Thalès et sa Réciproque : Comprendre et Appliquer

Explorez en profondeur le théorème de Thalès et sa réciproque. Cette ressource complète, conçue pour les élèves de lycée, offre des explications claires, des exemples concrets et des exercices pratiques pour maîtriser ces concepts fondamentaux de la géométrie plane.

Introduction au Théorème de Thalès

Le théorème de Thalès est un outil fondamental en géométrie qui nous permet de calculer des longueurs dans des configurations spécifiques impliquant des triangles semblables. Il est basé sur la proportionnalité des côtés de ces triangles. Configuration de Thalès: La configuration de Thalès se présente généralement sous deux formes principales :

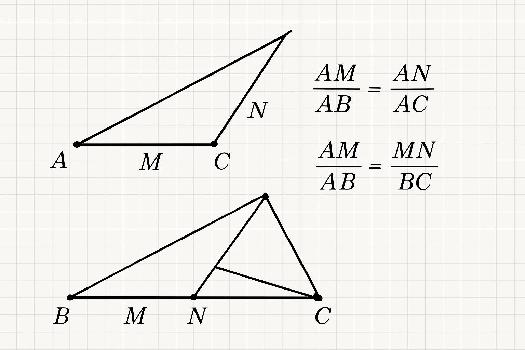
  • Triangles emboîtés (papillon): Deux triangles partagent un sommet commun, et les côtés opposés à ce sommet sont parallèles.
  • Triangles séparés : Deux triangles partagent un sommet commun, et les côtés opposés à ce sommet sont parallèles.

Énoncé du Théorème de Thalès

Soient deux droites (d) et (d') sécantes en un point A. Soient B et M deux points de (d), distincts de A, et C et N deux points de (d'), distincts de A. Si les droites (BC) et (MN) sont parallèles, alors on a l'égalité des rapports suivants :

AM / AB = AN / AC = MN / BC
Explication: Cette égalité signifie que les longueurs des segments correspondants des deux triangles AMN et ABC sont proportionnelles. Cela nous permet de calculer une longueur inconnue si on connait les autres.

Démonstration du Théorème de Thalès

La démonstration rigoureuse du théorème de Thalès nécessite des outils mathématiques plus avancés, notamment l'utilisation des propriétés des aires et des translations. Cependant, on peut l'illustrer de manière intuitive en considérant les triangles semblables et en observant la conservation des proportions entre leurs côtés. Illustration: Imaginez que vous agrandissez une photo sur un écran. Tous les éléments de la photo sont agrandis dans la même proportion. Le théorème de Thalès exprime une idée similaire : si vous 'agrandissez' un triangle tout en conservant le parallélisme de certains côtés, les rapports entre les longueurs des côtés restent constants.

Exemple d'Application du Théorème de Thalès

Exemple: Supposons que nous avons les données suivantes :

  • AM = 3 cm
  • AB = 7 cm
  • AN = 4 cm
  • BC = 10 cm
Nous cherchons à calculer la longueur de AC et MN. D'après le théorème de Thalès, on a :
3 / 7 = 4 / AC = MN / 10
Pour calculer AC, on utilise la première égalité : 3 / 7 = 4 / AC 3 * AC = 7 * 4 AC = 28 / 3 ≈ 9.33 cm Pour calculer MN, on utilise la première et la troisième égalité: 3 / 7 = MN / 10 3 * 10 = 7 * MN MN = 30 / 7 ≈ 4.29 cm Donc, AC mesure environ 9.33 cm et MN mesure environ 4.29 cm.

La Réciproque du Théorème de Thalès

La réciproque du théorème de Thalès permet de démontrer que deux droites sont parallèles. Elle est très utile pour vérifier si une configuration géométrique satisfait la condition de parallélisme. Énoncé de la réciproque: Soient deux droites (d) et (d') sécantes en un point A. Soient B et M deux points de (d), distincts de A, et C et N deux points de (d'), distincts de A. Si AM / AB = AN / AC , alors les droites (BC) et (MN) sont parallèles. Important: Pour appliquer correctement la réciproque, il est crucial de vérifier que les points A, B, M et A, C, N sont alignés dans le même ordre.

Exemple d'Application de la Réciproque

Exemple: Supposons que nous avons les données suivantes :

  • AM = 5 cm
  • AB = 8 cm
  • AN = 6 cm
  • AC = 9.6 cm
Nous voulons vérifier si les droites (BC) et (MN) sont parallèles. Calculons les rapports : AM / AB = 5 / 8 = 0.625 AN / AC = 6 / 9.6 = 0.625 Comme AM / AB = AN / AC et que les points A, B, M et A, C, N sont alignés dans le même ordre, alors d'après la réciproque du théorème de Thalès, les droites (BC) et (MN) sont parallèles.

Cas Particuliers et Pièges à Éviter

  • Ordre des points: Assurez-vous que les points sont alignés dans le même ordre pour appliquer la réciproque. Si l'ordre n'est pas respecté, la réciproque ne peut pas être utilisée.
  • Calcul des rapports: Vérifiez attentivement les calculs des rapports pour éviter les erreurs. Une erreur dans le calcul des rapports peut conduire à une conclusion fausse sur le parallélisme des droites.
  • Configurations complexes: Dans des configurations géométriques complexes, il peut être nécessaire de décomposer le problème en étapes plus simples et d'appliquer le théorème de Thalès ou sa réciproque plusieurs fois.

Ce qu'il faut retenir

  • Théorème de Thalès: Si (BC) // (MN), alors AM / AB = AN / AC = MN / BC. Ce théorème permet de calculer des longueurs.
  • Réciproque du Théorème de Thalès: Si AM / AB = AN / AC et que les points A, B, M et A, C, N sont alignés dans le même ordre, alors (BC) // (MN). Cette réciproque permet de démontrer que deux droites sont parallèles.
  • Configurations: Identifier correctement les configurations de Thalès (triangles emboîtés et triangles séparés).
  • Ordre des points: L'ordre des points est crucial pour appliquer la réciproque.

← Le Produit Scalaire : Guide Complet pour le Lycée Maîtriser le Produit Scalaire : Exercices et Applications Complexes →

FAQ

  • Quand puis-je utiliser le théorème de Thalès ?

    Vous pouvez utiliser le théorème de Thalès lorsque vous avez deux droites sécantes coupées par deux droites parallèles, formant ainsi deux triangles semblables.
  • Quelle est la différence entre le théorème de Thalès et sa réciproque ?

    Le théorème de Thalès permet de calculer des longueurs si les droites sont parallèles, tandis que sa réciproque permet de démontrer que des droites sont parallèles si une égalité de rapports est vérifiée.
  • Que se passe-t-il si les points ne sont pas alignés dans le même ordre lors de l'utilisation de la réciproque ?

    Si les points ne sont pas alignés dans le même ordre, vous ne pouvez pas appliquer la réciproque du théorème de Thalès pour conclure au parallélisme des droites.