Mathématiques > Géométrie > Géométrie Analytique > Étude de lieux géométriques (cercles, ellipses, hyperboles - notions)

Introduction aux Cercles, Ellipses et Hyperboles

Explorez les bases des cercles, des ellipses et des hyperboles en géométrie analytique. Apprenez leurs définitions, leurs équations et leurs propriétés fondamentales à travers des exemples clairs et concis.

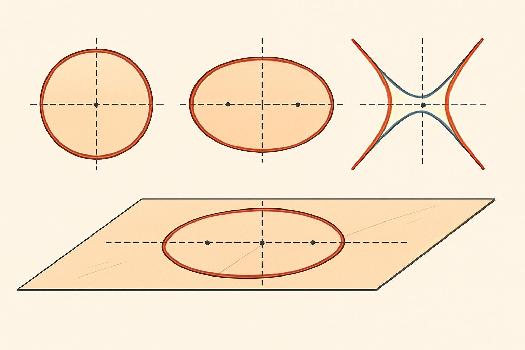
Le Cercle : Définition et Équation

Le cercle est l'ensemble des points situés à une distance constante (le rayon) d'un point fixe (le centre).

Définition : Un cercle de centre C(a, b) et de rayon r est l'ensemble des points M(x, y) tels que CM = r.

Équation cartésienne : L'équation cartésienne d'un cercle de centre C(a, b) et de rayon r est donnée par : (x - a)² + (y - b)² = r².

Exemple : Le cercle de centre (2, 3) et de rayon 5 a pour équation : (x - 2)² + (y - 3)² = 25.
Explication de l'equation:

  • (x-a) et (y-b) représentent les distances horizontales et verticales entre un point (x,y) du cercle et le centre (a,b).
  • En élevant ces distances au carré et en les additionnant, on obtient le carré de la distance entre le point (x,y) et le centre (a,b).
  • Cette somme est égale au carré du rayon (r²), ce qui garantit que tous les points (x,y) du cercle sont à une distance r du centre (a,b).

L'Ellipse : Définition et Équation

L'ellipse est l'ensemble des points dont la somme des distances à deux points fixes (les foyers) est constante.

Définition : Une ellipse de foyers F1 et F2 est l'ensemble des points M tels que MF1 + MF2 = 2a, où 2a est une constante (la longueur du grand axe).

Équation cartésienne : Si les foyers sont sur l'axe des x, l'équation de l'ellipse est : x²/a² + y²/b² = 1, où a est le demi-grand axe et b le demi-petit axe. La relation entre a, b et la distance focale c est : a² = b² + c².

Si les foyers sont sur l'axe des y, l'équation de l'ellipse est : y²/a² + x²/b² = 1, où a est le demi-grand axe et b le demi-petit axe.

Exemple : L'ellipse d'équation x²/25 + y²/9 = 1 a un demi-grand axe de longueur 5 et un demi-petit axe de longueur 3.
Eléments importants de l'ellipse:

  • Foyers: Deux points fixes F1 et F2 tels que la somme des distances de tout point de l'ellipse à ces foyers est constante.
  • Centre: Le milieu du segment reliant les foyers.
  • Grands Axe: Le segment de droite passant par les foyers et dont les extrémités sont sur l'ellipse. Sa longueur est 2a.
  • Petits Axe: Le segment de droite perpendiculaire au grand axe passant par le centre de l'ellipse, et dont les extrémités sont sur l'ellipse. Sa longueur est 2b.
  • Sommets: Les extrémités du grand axe et du petit axe.

L'Hyperbole : Définition et Équation

L'hyperbole est l'ensemble des points dont la différence des distances à deux points fixes (les foyers) est constante.

Définition : Une hyperbole de foyers F1 et F2 est l'ensemble des points M tels que |MF1 - MF2| = 2a, où 2a est une constante.

Équation cartésienne : Si les foyers sont sur l'axe des x, l'équation de l'hyperbole est : x²/a² - y²/b² = 1. Si les foyers sont sur l'axe des y, l'équation est : y²/a² - x²/b² = 1.

Asymptotes : Les asymptotes de l'hyperbole x²/a² - y²/b² = 1 sont les droites y = ±(b/a)x.

Exemple : L'hyperbole d'équation x²/16 - y²/9 = 1 a des asymptotes d'équations y = ±(3/4)x.
Eléments importants de l'Hyperbole:

  • Foyers: Deux points fixes F1 et F2 tels que la valeur absolue de la différence des distances de tout point de l'hyperbole à ces foyers est constante.
  • Centre: Le milieu du segment reliant les foyers.
  • Axe Transverse: Le segment de droite passant par les foyers et dont les extrémités sont sur l'hyperbole. Sa longueur est 2a.
  • Axe Conjugué: Le segment de droite perpendiculaire à l'axe transverse passant par le centre de l'hyperbole. Sa longueur est 2b.
  • Sommets: Les extrémités de l'axe transverse.
  • Asymptotes: Deux droites que l'hyperbole approche de plus en plus sans jamais les atteindre.

Résumé des Équations

Voici un tableau récapitulatif des équations des différentes coniques étudiées :

Conique Équation
Cercle (x - a)² + (y - b)² = r²
Ellipse x²/a² + y²/b² = 1 (si foyers sur l'axe des x) ou y²/a² + x²/b² = 1 (si foyers sur l'axe des y)
Hyperbole x²/a² - y²/b² = 1 (si foyers sur l'axe des x) ou y²/a² - x²/b² = 1 (si foyers sur l'axe des y)

Ce qu'il faut retenir

Cercle : Ensemble des points équidistants d'un centre. Équation : (x - a)² + (y - b)² = r².
Ellipse : Ensemble des points dont la somme des distances à deux foyers est constante. Équation : x²/a² + y²/b² = 1.
Hyperbole : Ensemble des points dont la différence des distances à deux foyers est constante. Équation : x²/a² - y²/b² = 1.
Bien comprendre la signification des paramètres a, b, et r dans les équations. Connaitre l'impact du centre dans l'equation du cercle.

← Introduction au repérage cartésien dans le plan Le Cercle Trigonométrique: Découverte et Applications →

FAQ

  • Comment reconnaître une ellipse d'une hyperbole à partir de leur équation ?

    Dans l'équation d'une ellipse, les termes x² et y² sont additionnés (x²/a² + y²/b² = 1), tandis que dans l'équation d'une hyperbole, ils sont soustraits (x²/a² - y²/b² = 1).
  • Quelle est la différence entre le grand axe et le petit axe d'une ellipse ?

    Le grand axe est le diamètre le plus long de l'ellipse, tandis que le petit axe est le diamètre le plus court. Le demi-grand axe est 'a' et le demi-petit axe est 'b'.