Mathématiques > Géométrie > Géométrie Plane > Distance entre deux points

Démonstration et applications avancées de la distance entre deux points

Explorez la démonstration rigoureuse de la formule de la distance entre deux points et découvrez ses applications avancées en géométrie, notamment pour prouver des propriétés géométriques. Cours adapté aux lycéens.

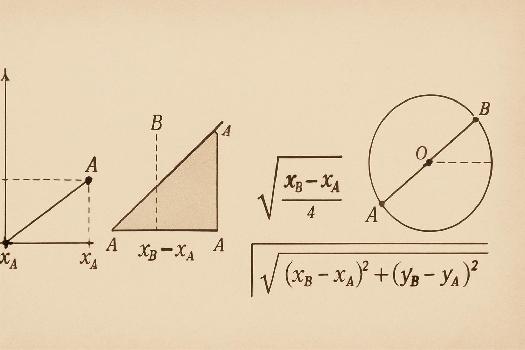
Rappel de la formule de la distance

Rappelons la formule de la distance entre deux points A(xA, yA) et B(xB, yB) dans un repère orthonormé :

AB = √((xB - xA)2 + (yB - yA)2)

Démonstration rigoureuse

La démonstration repose sur le théorème de Pythagore appliqué à un triangle rectangle construit à partir des points A et B. Considérons le point C de coordonnées (xB, yA). Le triangle ABC est rectangle en C.

Alors, d'après le théorème de Pythagore :

AB2 = AC2 + BC2

AC = |xB - xA| et BC = |yB - yA|

Donc, AB2 = (xB - xA)2 + (yB - yA)2

Et AB = √((xB - xA)2 + (yB - yA)2)

Il est important de noter que l'ordre des points A et B n'a pas d'importance car (xB - xA)2 = (xA - xB)2 et (yB - yA)2 = (yA - yB)2.

Applications avancées

La formule de la distance entre deux points est utilisée dans de nombreux problèmes de géométrie, notamment :

  • Calcul du périmètre d'un polygone : On calcule la distance entre chaque paire de sommets consécutifs, puis on additionne ces distances.
  • Vérification si un triangle est isocèle ou équilatéral : On calcule les longueurs des trois côtés et on compare.
  • Démonstration de l'alignement de trois points : Trois points A, B et C sont alignés si AB + BC = AC (ou une permutation de ces points).
  • Recherche de l'équation d'un cercle : L'équation d'un cercle de centre (a, b) et de rayon r est (x - a)2 + (y - b)2 = r2. Cette équation exprime que la distance entre un point (x, y) du cercle et le centre (a, b) est constante et égale au rayon r.

Exemples d'applications avancées

Exemple 1: Prouver que le triangle ABC est isocèle. Soient A(1, 2), B(4, 6) et C(7, 2). Calculons les longueurs des côtés:

AB = √((4 - 1)2 + (6 - 2)2) = √(9 + 16) = 5

BC = √((7 - 4)2 + (2 - 6)2) = √(9 + 16) = 5

AC = √((7 - 1)2 + (2 - 2)2) = √(36 + 0) = 6

Puisque AB = BC, le triangle ABC est isocèle en B.

Exemple 2: Vérifier si les points A(1, 1), B(3, 4) et C(5, 7) sont alignés.

AB = √((3 - 1)2 + (4 - 1)2) = √(4 + 9) = √13

BC = √((5 - 3)2 + (7 - 4)2) = √(4 + 9) = √13

AC = √((5 - 1)2 + (7 - 1)2) = √(16 + 36) = √52 = 2√13

Puisque AB + BC = √13 + √13 = 2√13 = AC, les points A, B et C sont alignés.

Exercices

Exercice 1: Déterminer si le triangle de sommets A(0, 0), B(4, 0) et C(2, 2√3) est équilatéral.

Exercice 2: Démontrer que les points A(-2, 1), B(1, 5) et C(4, 9) sont alignés.

Exercice 3: Trouver l'équation du cercle de centre (2, 3) et de rayon 5.

Ce qu'il faut retenir

  • La formule AB = √((xB - xA)2 + (yB - yA)2) est fondamentale.
  • Elle est une application du théorème de Pythagore.
  • Elle permet de résoudre des problèmes de géométrie tels que le calcul de périmètres, la vérification de la nature des triangles et la démonstration de l'alignement de points.
  • Elle est utilisée pour définir l'équation d'un cercle.

← Droites et plans dans l'espace : équations paramétriques et cartésiennes Exemples pratiques de résolution d'équations trigonométriques →

FAQ

  • Comment utiliser la formule de la distance pour déterminer si un quadrilatère est un parallélogramme?

    Un quadrilatère est un parallélogramme si ses côtés opposés sont de même longueur. Calculez la longueur de chaque côté en utilisant la formule de la distance, puis vérifiez si les côtés opposés ont des longueurs égales.
  • Comment trouver le milieu d'un segment à partir des coordonnées des extrémités?

    Le milieu M d'un segment [AB] avec A(xA, yA) et B(xB, yB) a pour coordonnées M((xA + xB)/2, (yA + yB)/2).